Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của NGUUYỄN NGỌC MINH - Toán lớp 9 - Học toán với OnlineMath

Ta có \(b\left(a^2-2\right)=a\left(ab+2\right)-2\left(a+b\right)\). Do \(a^2-2\vdots ab+2\) nên \(2\left(a+b\right)\vdots ab+2\to ab+2\le2a+2b\to\left(a-2\right)\left(b-2\right)\le2\).
Với \(a=1\to-\frac{1}{b+2}\in Z\), loại
Với \(a=2\to\frac{4}{2b+2}\in Z\to2b+2=4\to b=1\)
Với \(a=3\to\frac{7}{3b+2}\in Z\to3b+2=7\to\) loại
Với \(a=4\to\frac{14}{4b+2}\in Z\to4b+2=14\to b=3.\)
Với \(a\ge5\to b-2\le\frac{2}{a-2}<1\to b\le2\to b=1,2\). Với \(b=1\to\frac{a^2-2}{a+2}\in Z\to a-2+\frac{2}{a+2}\in Z\to a+2=2\to\) loại.
Nếu \(b=2\to\frac{a^2-2}{2a+2}\in Z\to\frac{a^2-2}{a+1}\in Z\to\frac{3}{a+1}\in Z\to a+1=3\to\) loại.
Vậy các cặp số \(\left(a,b\right)\) nguyên dương thoả mãn là \(\left(2,1\right);\left(4,3\right).\)

Đề đúng : tìm tất cả các số nguyên dương \(a,b\) sao cho \(a+b^2\) chia hết cho \(a^2b-1\)
Có thể vào đây tham khảo\(\rightarrow\) Các bài toán và vấn đề về Số học
de the nao lam nhu vay
Tra loi: tat ca cac so nguyen duong a,b deu thoa man

Vì gcd(x,x2+1)=1gcd(x,x2+1)=1 suy ra
Hoặc xy−1|;xxy−1|;x hoặc xy−1|x2+1xy−1|x2+1
Trường hợp 1 ta có: {x−1≤xy−1≤xxy−1|x}⇒[xy−1=xxy−1=1]⇒[x(y−1)=1xy=2]⇒[x=1;y=2x=2;y=1]{x−1≤xy−1≤xxy−1|x}⇒[xy−1=xxy−1=1]⇒[x(y−1)=1xy=2]⇒[x=1;y=2x=2;y=1]
Trường hợp 2 xét modulo xx ta có: {xy−1≡−1(modx)x2+1≡1(modx)}⇒−1≡1(modx)⇒2≡0(modx)⇒x=1 hoặc x=2{xy−1≡−1(modx)x2+1≡1(modx)}⇒−1≡1(modx)⇒2≡0(modx)⇒x=1 hoặc x=2
Thay các giá trị xx vào biểu thức ta tìm được yy
Cuối cùng các giá trị phải tìm là (x,y)∈{(1,2);(1,3);(2,1);(2,3)}(x,y)∈{(1,2);(1,3);(2,1);(2,3)}
k mik nha
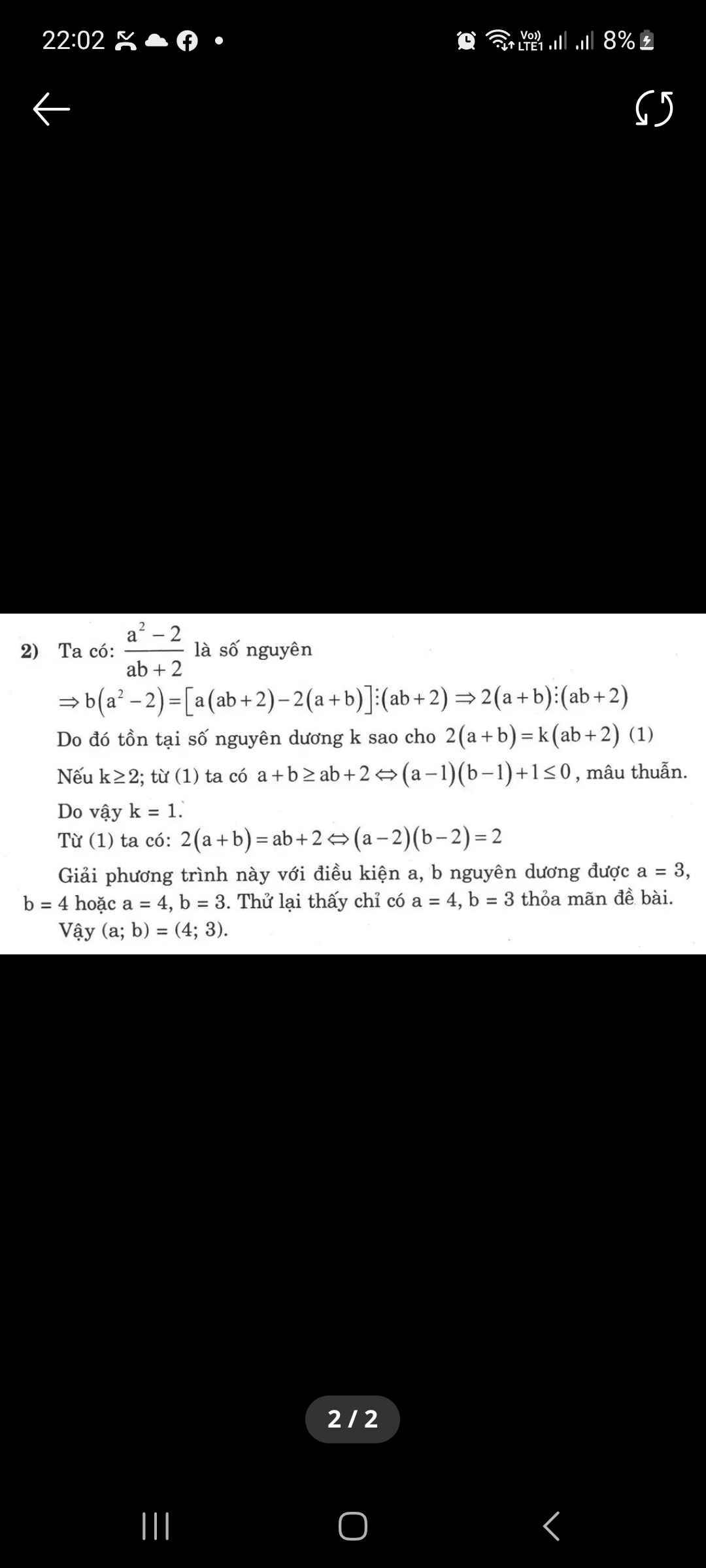
vào link này tham khảo : https://diendantoanhoc.net/topic/134969-tìm-tất-cả-các-cặp-số-nguyên-dương-a-và-b-sao-cho-fraca2-2ab2-là-số-nguyên/