
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



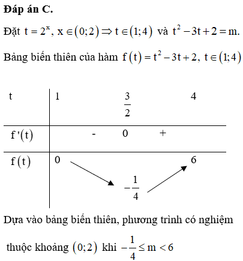
Đáp án C
6 x − 3 − m 2 x − m = 0 ⇔ m = 6 x + 3.2 x 2 x + 1
Xét hàm số f x = 6 x + 3.2 x 2 x + 1 trên khoảng 0 ; 1
f ' x = 6 x .2 x ln 6 − ln 2 + 6 x ln 6 + 3.2 x ln 2 2 x + 1 2 > 0 do đó hàm số y = f x đồng biến trên khoảng 0 ; 1 .
Phương trình f x = m có nghiệm trong khoảng 0 ; 1 ⇔ f 0 < m < f 1 ⇔ 2 < m < 4 .

Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
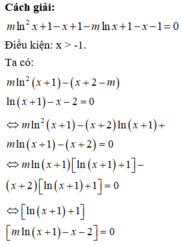
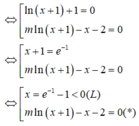

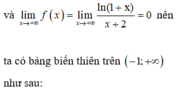


Đáp án A
Điều kiện x ≥ − 2
Đặt t = x + 2 t ≥ 0 ⇒ x = t 2 − 2
Khi đó phương trình tương đương
5 − t 2 + t + 2 − 5 m = 0 ⇔ m = 5 − t 2 + t + 1
Xét hàm số f t = 5 − t 2 + t + 1 ; t ≥ 0.
Ta có:
f ' t = − 2 t + 1 5 − t 2 + t + 1 ; f ' t = 0 ⇔ t = 1 2
Từ bảng biến thiên ra suy ra phương trình có nghiệm thì 0 < m ≤ 5 5 4

Đặt t=2sinx+1 với
![]()
![]()
![]()
Phương trình trở thành: f(t)=m có nghiệm ![]()
Chọn đáp án A.

Đáp án B.
Đặt t = log 2 x , khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 ⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt ⇔ a = m + 1 ≠ 0 ∆ ' = 1 - m + 1 m - 2 > 0 ⇔ m ≠ - 1 m 2 - m - 3 < 0 1 .
Khi đó gọi x 1 ; x 2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x 1 < 1 < x 2 suy ra t 1 = log 2 x 1 < 0 t 2 = log 2 x 2 > 0 ⇒ t 1 t 2 = c a = m - 2 m + 1 < 0 2 .
Từ (1), (2) suy ra - 1 < m < 2 ⇔ m ∈ - 1 ; 2 là giá trị cần tìm.