Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.

Đáp án B.
Điều kiện: x , y , z > 0 ; x ∈ ℕ .
Theo tính chất của cấp số cộng ta có:
2 log 12 x = log 12 162 + log 12 y 2 log 12 y = log 12 x + log 12 z 2 log 12 z = log 12 y + log 12 1250 ⇔ x 2 = 162 y y 2 = x z z 2 = 1250 y
⇒ x y z 2 = 162.1250. x y 2 z ⇒ x z = 202500 ⇒ y 2 = 202500 ⇒ y = 450
⇒ x 2 = 162450 ⇒ x = 270
Vậy tổng các chữ số của x là 9.
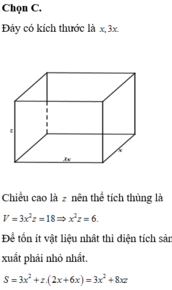
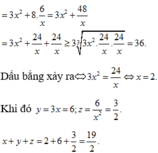
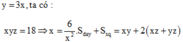
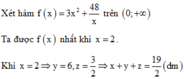
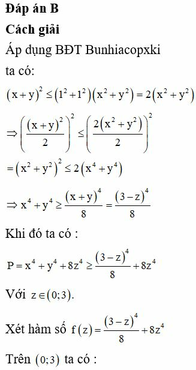

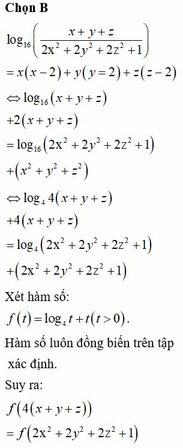


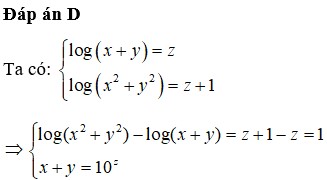
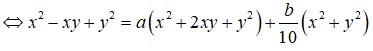
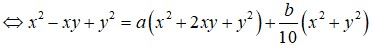
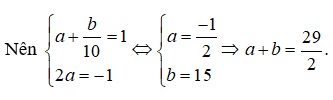

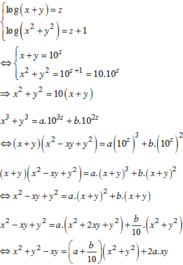
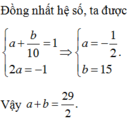
Dễ thấy x là số có hai chữ số. Gọi x=ab¯=10a+b,y=a+b.
Có hai trường hợp đối với z:
- Nếu y=a+b≤9 thì z=a+b.
- Nếu y=a+b≥10 thì z=a+b−9.
a) Trường hợp a+b≤9 thì (10a+b)+(a+b)+(a+b)=60. Suy ra 4a+b=20.
Ta thấy b⋮4. Thay b = 0, 4, 8, tương ứng ta được a = 5, 4, 3. Loại trường hợp b = 8, a = 3 vìa+b>9.
b) Trường hợp a+b≥10 thì (10a+b)+(a+b)+(a+b−9)=60 suy ra 4a + b = 23. Ta được a = 4, b = 7.
Kết luận: có ba số 44, 47, 50 thỏa mãn đề bài.
Dễ thấy x là số có hai chữ số. Gọi x=ab¯=10a+b,y=a+b.
Có hai trường hợp đối với z:
- Nếu y=a+b≤9 thì z=a+b.
- Nếu y=a+b≥10 thì z=a+b−9.
a) Trường hợp a+b≤9 thì (10a+b)+(a+b)+(a+b)=60. Suy ra 4a+b=20.
Ta thấy b⋮4. Thay b = 0, 4, 8, tương ứng ta được a = 5, 4, 3. Loại trường hợp b = 8, a = 3 vìa+b>9.
b) Trường hợp a+b≥10 thì (10a+b)+(a+b)+(a+b−9)=60 suy ra 4a + b = 23. Ta được a = 4, b = 7.
Kết luận: có ba số 44, 47, 50 thỏa mãn đề bài.