Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi ba chữ số của số phải tìm là a, b, c
![]()
Số phải tìm là bội của 18 nên số đó chia hết cho 9 , do đó a + b + c= 9 hoặc a + b + c = 18 hoặc a + b + c =27
Theo đề bài, các chữ số của số đó tỉ lệ với 1;2;3 nên
a 1 = b 2 = c 3
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
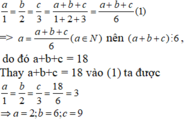
Lại có số phải tìm là bội của 18 nên chữ số hàng đơn vị của nó là số chẵn, do đó có hai số thỏa mãn đề bài là 396;936
Đáp án cần chọn là C

Do số cần tìm chia hết cho18 nên nó chia hết cho 2 và 9
=> chữ số tận cùng của số đó là số chẵn và tổng các chữ số của số đó chia hết cho 9
Do các chữ số tỷ lệ theo 1:2:3 thì có các bộ là (1; 2; 3), (2; 4; 6), (3; 6; 9)
Tổng các chữ số chia hết cho 9 thì chỉ có bộ (3; 6; 9) thỏa mãn
Do chữ số cuối cùng là chẵn nên chữ số hàng đơn vị là 6
Số cần tìm là 936 hoặc 396

Gọi các c/s được chia ra bởi số phải tìm lần lượt là a , b , c ( a , b ,c > 0 )
Theo bài ra ta có :
- Do số đó là bội của 18 nên số đó chia hết cho 9 ( abc chia hết 9 và 2 )
nên : a + b + c thuộc { 9 , 18 , 27 } ( 1 )
- \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{1+2+3}=\frac{a+b+c}{6}\) ( áp dụng tính chất dãy tỉ số bằng nhau)
Do a + b + c là STN nên a + b + c chia hết cho 6 ( 2 )
Từ ( 1 ) và ( 2 ) nên a + b +c = 18
suy ra \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{18}{6}=3\)
nên a = 1. 3 = 3 , b = 2 .3 =6 , c = 3 . 3 = 9
Kết quả ra 6 TH : 369 . 396 . 693 , 639 , 936 , 963
mà abc chia hết cho 2 ( abc là bội của 18 )
nên abc = 396 hoặc abc = 936
Vậy số phải tìm là 936 hoặc 396

Gọi các chữ số của số đó là \(a,b,c\left(a< b< c\right)\)
Theo đề bài , ta có : \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)
Vì số đó là bội của 27 nên cũng là bội của 9 \(\Rightarrow a+b+c⋮9\) \(\left(1\right)\)
Có \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)\(\Rightarrow\frac{a}{1}+\frac{b}{2}+\frac{c}{3}=\frac{a+b+c}{6}\)
Ta có : \(\frac{a}{1}\)là số nguyên nên \(a+b+c⋮6\) \(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow a+b+c\in BC\left(9;6\right)=B\left(18\right)\)
Ta có : \(3\le a+b+c\le27\)nên \(a+b+c=18\)
\(\Rightarrow\frac{q}{1}=\frac{b}{2}=\frac{c}{3}=\frac{18}{6}=3\)
\(\Rightarrow a=3;b=6;c=9\)
Vậy số cần tìm là 369

Gọi chữ số nhỏ nhất là x
=> Ba chữ số theo tỉ lệ là: x, 2x, 3x với 3x ≤ 9
=> x ≤ 3 (1)
Vì số cần tìm chia hết cho 18, nghĩa là chia hết cho 9
Nên (x + 2x + 3x) = 6x chia hết cho 9
=> x chia hết cho 3 (2)
Từ (1) & (2), suy ra: x = 3
=> Ba chữ số là 3, 6, 9
Theo đề bài số cần tìm chia hết cho 18 (18 là số chẵn), nghĩa là chia hết cho 2, vậy chữ số cuối phải là 6
=> Số cần tìm là 396 hoặc 936

Gọi số cần tìm có dạng \(\overline{abc}\). \(\left(0\le a,b,c\le9\right)\),
Do \(a:b:c=1:2:3\) nên ta chỉ có hai trường hợp:
\(\overline{abc}=123,\overline{abc}=246\) , \(\overline{abc}=369\).
Trong tất cả các số trên đều không có só nào chia hết cho 18. Vậy tập hợp các số tìm được là rỗng.

gọi 3 chữ số của số cần tìm là a,b,c ( a,b,c \(\in\)N ; a\(\ne\)0, a,b,c, \(\le\)9 )
Theo đầu bài ta có :
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)\(\Rightarrow\frac{a}{1}=\frac{a+b+c}{1+2+3}\)\(\Rightarrow a=\frac{a+b+c}{6}\)
Do vậy : a + b + c \(⋮\)6 ( 1 )
Mặt khác số đó chia hết cho 18 nên số đó chia hết cho 9 \(\Rightarrow\)a + b + c \(⋮\)9 ( 2 )
Mà 0 < a + b + c \(\le\)27 ( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ) \(\Rightarrow\)a + b + c \(⋮\)18
Ta có : \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=3\)\(\Rightarrow a=3,b=6,c=9\)
\(\Rightarrow\)số đó là 396 hoặc 936

Gọi a, b,c lần lượt tỉ lệ với 1,2,3
a/1=b/2=c/3 và a+b+c=18
Áp dụng tính chất dãy tiwr số bằng :
a/1=b/2=c/3=a+b+c/1+2+3=18/6=3
Suy ra :a/1=3=>a=3
b/2=3=>b=6
c/3=3=>c=9