
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng tính chất “Trong tam giác vuông, hai góc nhọn phụ nhau” ta có:
+ Hình 55:

+ Hình 56:

+ Hình 57 :

+ Hình 58:
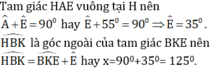

(x + 1)/58 + (x + 2)/57 = (x + 3)/56 + (x + 4)/55
(x + 1)/58 + 1 + (x + 2)/57 + 1 = (x + 3)/56 + 1 + (x + 4)/55 + 1
(x + 59)/58 + (x + 59)/57 = (x + 59)/56 + (x + 59)/55
=> (x + 59)/58 + (x + 59)/57 - (x + 59)/56 - (x + 59)/55 = 0
=> (x + 59).(1/58 + 1/57 - 1/56 - 1/55) = 0
Do 1/56 > 1/58; 1/55 > 1/57 => 1/58 + 1/57 - 1/56 - 1/55 khác 0
=> x + 59 = 0
=> x = -59
(x + 1)/58 + (x + 2)/57 = (x + 3)/56 + (x + 4)/55
(x + 1)/58 + 1 + (x + 2)/57 + 1 = (x + 3)/56 + 1 + (x + 4)/55 + 1
(x + 59)/58 + (x + 59)/57 = (x + 59)/56 + (x + 59)/55
=> (x + 59)/58 + (x + 59)/57 - (x + 59)/56 - (x + 59)/55 = 0
=> (x + 59).(1/58 + 1/57 - 1/56 - 1/55) = 0
Do 1/56 > 1/58; 1/55 > 1/57 => 1/58 + 1/57 - 1/56 - 1/55 khác 0
=> x + 59 = 0
=> x = -59

Ta có:
1+2+3-4-5-6+7+8+9-..........+55+56+57-58-59-60
=(1+2+3-4-5-6)+(7+8+9-10-11-12)..........+(55+56+57-58-59-60)
= -3+ (-3)+...+(-3)
---12 số------------
=(-3).12
=-36

\(\frac{x-1}{59}+\frac{x-2}{58}+\frac{x-3}{57}=\frac{x-4}{56}+\frac{x-5}{55}+\frac{x-6}{54}\)
<=>\(\frac{x-1}{59}+\frac{x-2}{58}+\frac{x-3}{57}-\frac{x-4}{56}-\frac{x-5}{55}-\frac{x-6}{54}=0\)
<=>\(\frac{x-1}{59}-1+\frac{x-2}{58}-1+\frac{x-3}{57}-1-\frac{x-4}{56}+1-\frac{x-5}{55}+1-\frac{x-6}{54}+1=0\)
<=>\(\frac{x-60}{59}+\frac{x-60}{58}+\frac{x-60}{57}-\frac{x-60}{56}-\frac{x-60}{55}-\frac{x-60}{54}=0\)
<=>\(\left(x-60\right)\left(\frac{1}{59}+\frac{1}{58}+\frac{1}{57}-\frac{1}{56}-\frac{1}{55}-\frac{1}{54}\right)=0\)
Do \(\frac{1}{59}+\frac{1}{58}+\frac{1}{57}-\frac{1}{56}-\frac{1}{55}-\frac{1}{54}\ne0\)
=>x-60=0
<=>x=60
Vậy x=60

Do trong hình có 2 đường thẳng cùng vuông góc với một đường thẳng nên 2 đt đó // với nhau
Do đó \(x+115^0=180^0\) (2 góc ở vị trí trong cùng phía)
Vậy \(x=180^0-115^0=65^0\)

Trả lời:
Hình 57:
Ta có: \(\widehat{M_1}+\widehat{M_2}=90^0\),
\(\widehat{N}+\widehat{M_2}=90^0\),
Suy ra \(\widehat{N}=\widehat{M_1}\)
Vậy \(\widehat{M_1}=60^0\)
Hình 58:
Ta có:
\(\widehat{E}=90^0-\widehat{A}=90^0-55^0=35^0\)
\(\widehat{B_1}=90^0+\widehat{E}\) (Góc ngoài tam giác BKE)
= 900 + 350 = 1250
Vậy ...
Chúc bạn học tốt!
Hình 55
\(\widehat{A}+\widehat{AIH}=90^0\)
\(x+\widehat{BIK}=90^0\)
mà \(\widehat{AIH}=\widehat{BIK}\) ( đối đỉnh )
\(\Rightarrow\widehat{A}=x\)
Hình 57
Xét \(\Delta ABD\) cân tại \(D\) ta có \(\Delta ABD+\Delta BAD=90^0\)
Xét \(\Delta ACE\) cân tại \(E\) ta có \(\Delta ACE+\Delta EAC=90^0\)
mà ta có \(\Delta ABD\) cũng chính là góc \(\Delta EAC\)
\(\Rightarrow\Delta ABD=\Delta ACE=25^0\)
Vậy \(\Delta ABD=25^0\Rightarrow x=25^0\)
Chúc bạn học tốt!

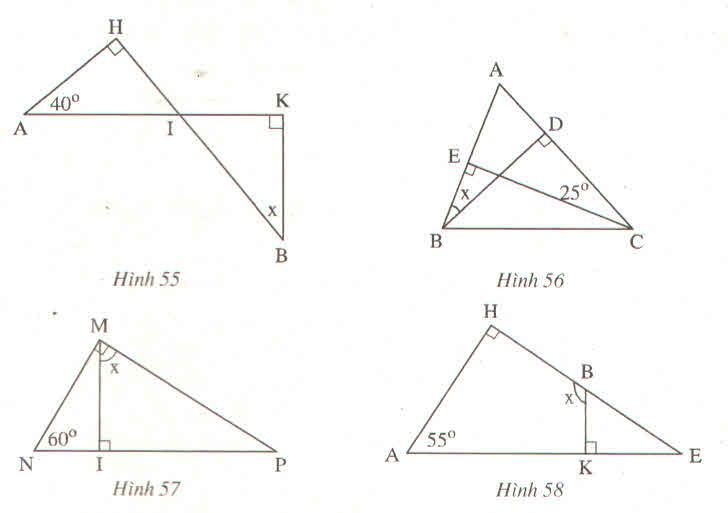

Hình 55:
Ta có ∠A + ∠AIH = 900 (Vì tam giác AHI cân tại H) ⇒∠AIH = 900 – 400 = 500
mà ∠AIH = ∠BIK( 2 góc đối đỉnh) ⇒∠BIK = 500
Ta lại có: ∠IBK +∠BIK = 900 (Vì tam giác IKB cân tại K)
⇒ ∠IBK = 900 – 500 = 400
⇒ x = 400
Hình 56:
Các em có thể giải theo cách của bài 55 tuy nhiên là hơi dài và chúng ta có cách khác làm nhanh hơn. (Áp dụng hình 56 và các hình sau nhé)
Ta có :
Xét tam giác ABD cân tại D ta có ∠ABD + ∠BAD = 900
Xét tam giác ACE cân tại E ta có ∠ACE + ∠EAC = 900
Mà ta có ∠BAD cũng chính là góc ∠EAC
Suy ra ∠ABD = ∠ACE = 250
Vậy ∠ABD = 250 => x = 250
Hình 57:
Xét tam giác MNP vuông tại M ⇒ ∠MNP+ ∠MPN = 900
⇔ 600 + ∠MPN = 900
⇒ ∠MPN = 900 – 600 = 300
Tiếp tục xét tam giác IMP vuông tại I ⇒ ∠IMP + ∠IPM = 900
⇔ ∠IMP + 300 = 900 ( vì∠IPM = ∠MPN )
⇒∠IMP = 900 – 300 = 600
Vậy ∠IMP = 600 => x = 600
Hình 58:
Ta có
Xét tam gác HAE vuông tại H nên ta có ∠HEA = 900 – ∠HAE = 900 – 550 = 350
hay chính là góc ∠BEK = 350
Ta có: ∠HBK = ∠BEK + ∠BKE (Góc ngoài tam giác BKE)
⇒ ∠HBK = 350+ 900 = 1250
Vậy x = 1250