
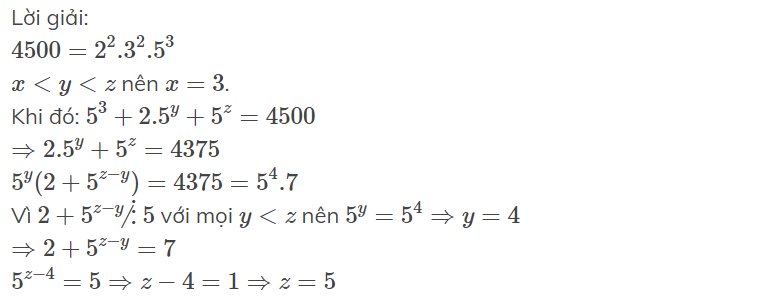
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

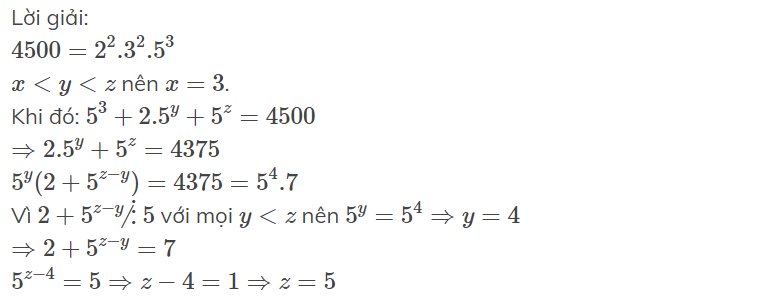

Lời giải:
$4500=2^2.3^2.5^3$
$x< y< z$ nên $x=3$.
Khi đó: $5^3+2.5^y+5^z=4500$
$\Rightarrow 2.5^y+5^z=4375$
$5^y(2+5^{z-y})=4375=5^4.7$
Vì $2+5^{z-y}\not\vdots 5$ với mọi $y< z$ nên $5^y=5^4\Rightarrow y=4$
$\Rightarrow 2+5^{z-y}=7$
$5^{z-4}=5\Rightarrow z-4=1\Rightarrow z=5$

Ta có : \(\left(5x+5y+5z\right)^2-\left(25xy+25yz+25zx\right)\)
\(=25\left(\left(x+y+z\right)^2-\left(xy+yz+zx\right)\right)\)
Xét : \(\left(x+y+z\right)^2-\left(xy+yz+zx\right)=0\)
\(=>x^2+y^2+z^2+2xy+2yz+2zx-xy-yz-zx=0\)
\(=>x^2+y^2+z^2+xy+yz+zx=0\)
Nhân biểu thức với 2 ta được:
\(2x^2+2y^2+2z^2+2xy+2yz+2zx=0\)
\(=>\left(x+y\right)^2+\left(y+z\right)^2+\left(z+x\right)^2=0\)
\(=>x+y=y+z=z+x=0\)
Vạy để phân thức A xác định thì x,y,z không đồng thời bằng 0;
CHÚC BẠN HỌC TỐT...

Không mất tính tổng quát, giả sử \(x\ge y\ge z\ge1\).
Khi đó ta có: \(13=xyz+x^2+y^2+z^2\ge z^3+3z^2\)
suy ra \(z=1\).
\(12=xy+x^2+y^2\ge y^2+y^2+y^2=3y^2\)
\(\Rightarrow y=1\)hoặc \(y=2\).
Với \(y=1\): \(x^2+1+1+x=13\Leftrightarrow x^2+x-11=0\)không có nghiệm nguyên dương.
Với \(y=2\): \(x^2+2^2+1^2+1.2.x=13\Leftrightarrow x^2+2x-8=0\Leftrightarrow\left(x-2\right)\left(x+4\right)=0\)
\(\Rightarrow x=2\)thỏa mãn.
Vậy phương trình có nghiệm là \(\left(1,2,2\right)\)và các hoán vị.