
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(PT\Leftrightarrow\left(x+y\right)\left(x+3y\right)-2\left(x+y\right)-5=0\)
\(\Leftrightarrow\left(x+y\right)\left(x+3y-2\right)=5\)
=> phương trình ước số

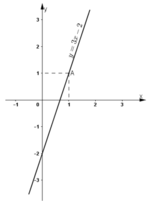
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
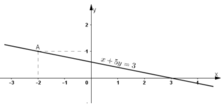
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
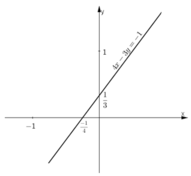
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 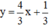
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
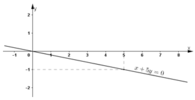
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ 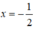
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
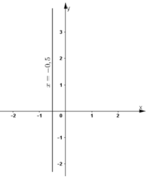
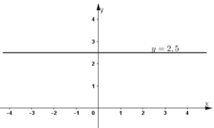
f) 0x + 2y = 5
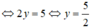
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.

\(\Leftrightarrow\left(x^2y^4-16xy^3+64y^2\right)+\left(4y^2-4xy+x^2\right)=0\)
\(\Leftrightarrow\left(xy^2-8y\right)^2+\left(2y-x\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy^2-8y=0\\2y-x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy^2-8y=0\\x=2y\end{matrix}\right.\)
\(\Rightarrow2y.y^2-8y=0\)
\(\Leftrightarrow2y\left(y^2-4\right)=0\Rightarrow\left[{}\begin{matrix}y=0\Rightarrow x=0\\y=2\Rightarrow x=4\\y=-2\Rightarrow x=-4\end{matrix}\right.\)

\(x^2+y^2=2x^2y^2\)
\(\Rightarrow\frac{x^2+y^2}{x^2y^2}=2\)
\(\Rightarrow\frac{1}{x^2}+\frac{1}{y^2}=2\left(1\right)\)
Do x,y bình đẳng như nhau,giả sử \(x\ge y\)
\(\Rightarrow x^2\ge y^2\)
Với x<1 thì VT của (1) âm mà vế phải dương.(Loại)
Với x=1 thì thỏa mãn
Với x>1 thì dễ thấy KTM
Vậy....

Pt đã cho đưa về dạng
(2x+y)^2 + 2(2x+y) + 1 + x^2 - 4 = 0
<=> (2x+y+1)^2 + x^2 = 4
Mà 4 = 0 + 2^2 = 0 + (-2)^2
Xét các TH là ra
(2x+y)^2 + 2(2x+y) + 1 + x^2 - 4 = 0
<=> (2x+y+1)^2 + x^2 = 4
Mà 4 = 0 + 2^2 = 0 + (-2)^2
Xét các TH là ra