Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(x^2+y^2+z^2=2xyz\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+z^2=0\)
\(\Leftrightarrow\left(x-y\right)^2+x^2=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x-y=0\\z=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=y\\z=0\end{array}\right.\)


Cách 1 (đồ thị): Đầu tiên ta xác định miền nghiệm của hệ bất phương trình sau: \(\left\{{}\begin{matrix}x>0\\y>0\\\dfrac{x}{3}+\dfrac{y}{4}\le1\end{matrix}\right.\) như sau:
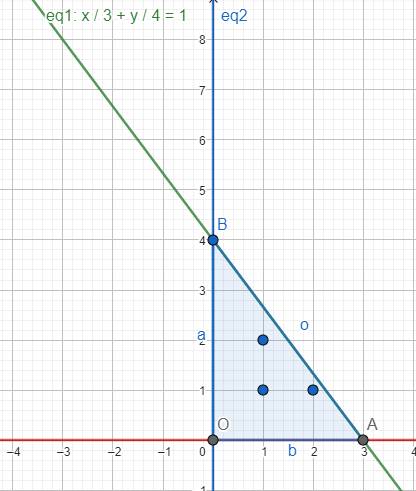
Sau đó ta tìm tất cả các điểm nguyên nằm ở miền trong tam giác OAB. Ta nhận thấy các điểm này là \(\left(1,1\right);\left(1,2\right);\left(2,1\right)\). Vậy các nghiệm (x; y) của bpt là \(\left(1;1\right),\left(1;2\right),\left(2;1\right)\)
Cách 2: (đại số)
Ta có \(\dfrac{x}{3}+\dfrac{y}{4}\le1\) nên \(\dfrac{x}{3}< 1\) \(\Leftrightarrow x< 3\) \(\Rightarrow x\in\left\{1,2\right\}\)
\(\dfrac{y}{4}< 1\Rightarrow y< 4\Rightarrow y\in\left\{1,2,3\right\}\)
Thử lại, ta thấy chỉ có các cặp \(\left(x;y\right)=\left(1;1\right),\left(1;2\right),\left(2;1\right)\) là thỏa mãn. Vậy...

bài 1
coi bậc 2 với ẩn x tham số y D(x) phải chính phường
<=> (2y-3)^2 -4(2y^2 -3y+2) =k^2
=> -8y^2 +1 =k^2 => y =0
với y =0 => x =-1 và -2

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

\(\Leftrightarrow\left(2x^2-3\right)y=x^2+1\)
\(\Leftrightarrow y=\dfrac{x^2+1}{2x^2-3}\)
\(y\in Z\Rightarrow2y\in Z\Rightarrow\dfrac{2x^2+2}{2x^2-3}\in Z\Rightarrow1+\dfrac{5}{2x^2-3}\in Z\)
\(\Rightarrow2x^2-3=Ư\left(5\right)=\left\{-1;1;5\right\}\)
\(\Rightarrow x^2=\left\{1;2;4\right\}\Rightarrow x=\left\{1;2\right\}\)
- Với \(x=1\Rightarrow y=-2< 0\left(loại\right)\)
- Với \(x=2\Rightarrow y=1\)
Vậy \(\left(x;y\right)=\left(2;1\right)\)