
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu hỏi của Phùng Gia Bảo - Toán lớp 9 - Học toán với OnlineMath

Câu hỏi của Phùng Gia Bảo - Toán lớp 9 - Học toán với OnlineMath

ý bạn a và b là 1 hệ pt hả chứ để riêng sao giải. Nếu giải hệ thì là như sau:
5x-y=13<=> y=5x-13. Thay vào pt b ta có: 23x+53(5x-13)=109 <=> 23x+265x=109+53.13. đến đây bạn tự giải

2 x + 3 y = − 2 3 x − 2 y = − 3 ⇔ 4 x + 6 y = − 4 9 x − 6 y = − 9 ⇔ 13 x = − 13 2 x + 3 y = − 2 ⇔ x = − 1 y = 0
Vậy hệ đã cho có nghiệm duy nhất (x; y) = (−1; 0)
x – y = −1 – 0 = −1
Đáp án: A

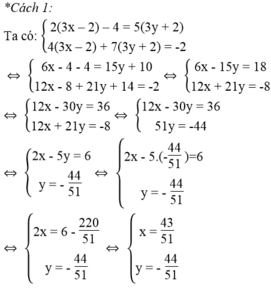
Vậy hệ phương trình đã cho có nghiệm (x; y) = (43/51 ; -44/51 )
*Cách 2: Đặt m = 3x – 2, n = 3y + 2
Ta có hệ phương trình:
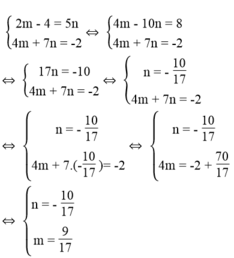
Ta có: 3x – 2 = 9/17 ⇔ 3x = 2 + 9/17 ⇔ 3x = 43/17 ⇔ x = 43/51
3y + 2 = - 10/17 ⇔ 3y = -2 - 10/17 ⇔ 3y = - 44/17 ⇔ y = - 44/51
Vậy hệ phương trình đã cho có nghiệm (x; y) = (43/51 ; -44/51 )

a)
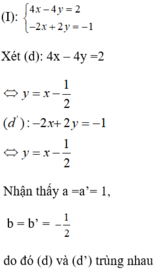
Vậy hệ phương trình có vô số nghiệm.
b)
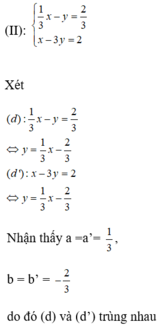
Vậy hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 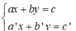
Gọi (d): ax + b = c và (d’): a’x + b’ = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’

a) Ta có: \(\Delta=2^2-4\cdot m\cdot3=4-12m\)
Để phương trình có nghiệm kép thì \(\Delta=0\)
\(\Leftrightarrow4-12m=0\)
\(\Leftrightarrow12m=4\)
hay \(m=\dfrac{1}{3}\)
Thay \(m=\dfrac{1}{3}\) vào phương trình, ta được:
\(\dfrac{1}{3}x^2+2x+3=0\)
\(\Leftrightarrow x^2+6x+9=0\)
\(\Leftrightarrow\left(x+3\right)^2=0\)
\(\Leftrightarrow x+3=0\)
hay x=-3
b) Để phương trình có nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow4-12m\ge0\)
\(\Leftrightarrow-12m\ge-4\)
hay \(m\le\dfrac{1}{3}\)
a) \(2x+3y+5z=15\)
Vì (2; 3; 5 ) =1
=> Phương trình sẽ có nghiệm nguyên.
\(pt\Leftrightarrow2x+5z=15-3y\)
Đặt: 15 - 3 y = a
Phương trình trở thành: \(2x+5z=a\) (1)
Phương trình (1) có 1 nghiệm là: x = -2a và z = a
=> Phương trình (1) có ngiệm tổng quát là: x = - 2a - 5t ; z = a + 2t (2)
Thế a = 15 -3y vào (2). Ta có: x = -2 (15-3y ) -5t = -30 + 6y - 5t và z = 15-3y +2t
Vậy phương trình trên có nghiệm:
\(\hept{\begin{cases}x=-30+6y-5t\\z=15-3y+2t\\y,t\in Z\end{cases}}\)
Bài b/ tương tự.