
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\widehat{xOM}+\widehat{xON}=40^0+140^0=180^0\) nên M,O,N thẳng hàng
Mà x,O,x' thẳng hàng nên \(\widehat{xON}\) đối đỉnh \(\widehat{x'OM}\)

Bài 1:
a: \(k=\dfrac{y}{x}=\dfrac{y_1}{x_1}=\dfrac{2}{3}\)
=>\(y=\dfrac{2}{3}x\)
b: Khi \(x_2=9\) thì \(y_2=\dfrac{2}{3}\cdot x_2=\dfrac{2}{3}\cdot9=6\)
c: Khi \(y_3=8\) thì \(\dfrac{2}{3}\cdot x_3=8\)
=>\(x_3=8:\dfrac{2}{3}=12\)
Bài 2:
a: x,y tỉ lệ thuận
nên \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{6}{y_2}=\dfrac{4}{9}\)
=>\(y_2=6\cdot\dfrac{9}{4}=\dfrac{3}{2}\cdot9=\dfrac{27}{2}\)
b: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{2}{-10}=-\dfrac{1}{5}\)
=>\(\dfrac{x}{y}=-\dfrac{1}{5}\)
=>y=-5x

a)Xét tam giác ABC vuông tại A có:
\(AB^2+AC^2=BC^2\left(Pitago\right)\)
=>\(BC^2=3^2+4^2=+16=25=5^2\)
=>BC=5cm
b)Xét tam giác ABC vuông tại A có
AD là đường trung tuyến ứng với cạnh huyền
=>\(AD=\dfrac{1}{2}BC=BD\)
=>\(\Delta ABD\) cân
Ta có :\(\widehat{BAH}+\widehat{ABH}=90\) độ(tam giác ABH vuông)
\(\widehat{ACB}+\widehat{ABC}=90\) độ(tam giác ABC vuông)
Mà 2 góc ABH và ABC là 1
=>\(\widehat{BAH}=\widehat{ACB}\)

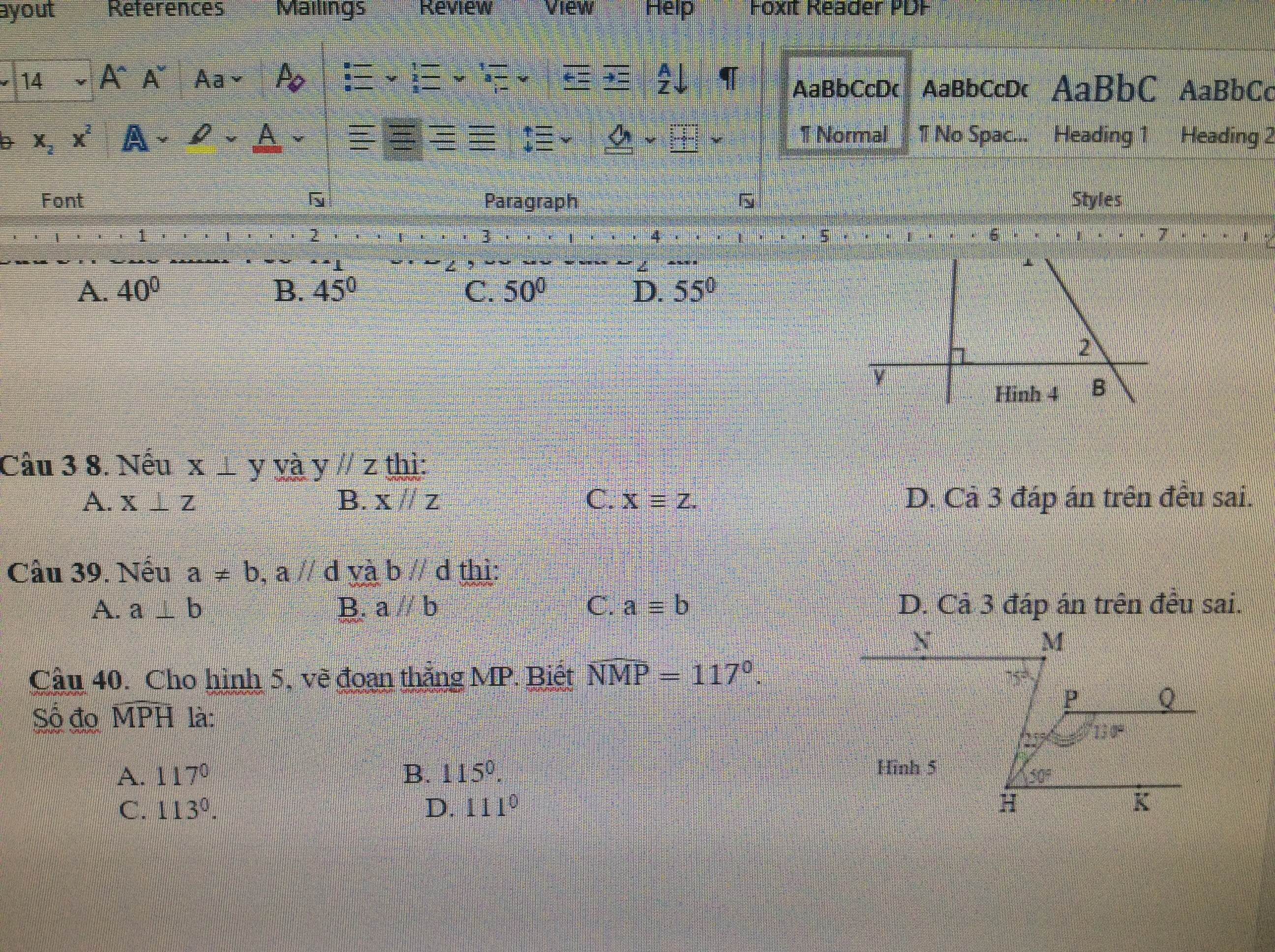
a: y=60+40=100 độ
b: x=40+70=110 độ
y=180-110-40=30 độ
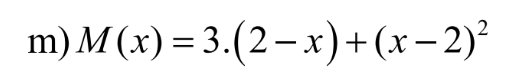


 Mik cần gấp ạaa
Mik cần gấp ạaa giúp em với ạaa
giúp em với ạaa cứu emm vs ạaa
cứu emm vs ạaa
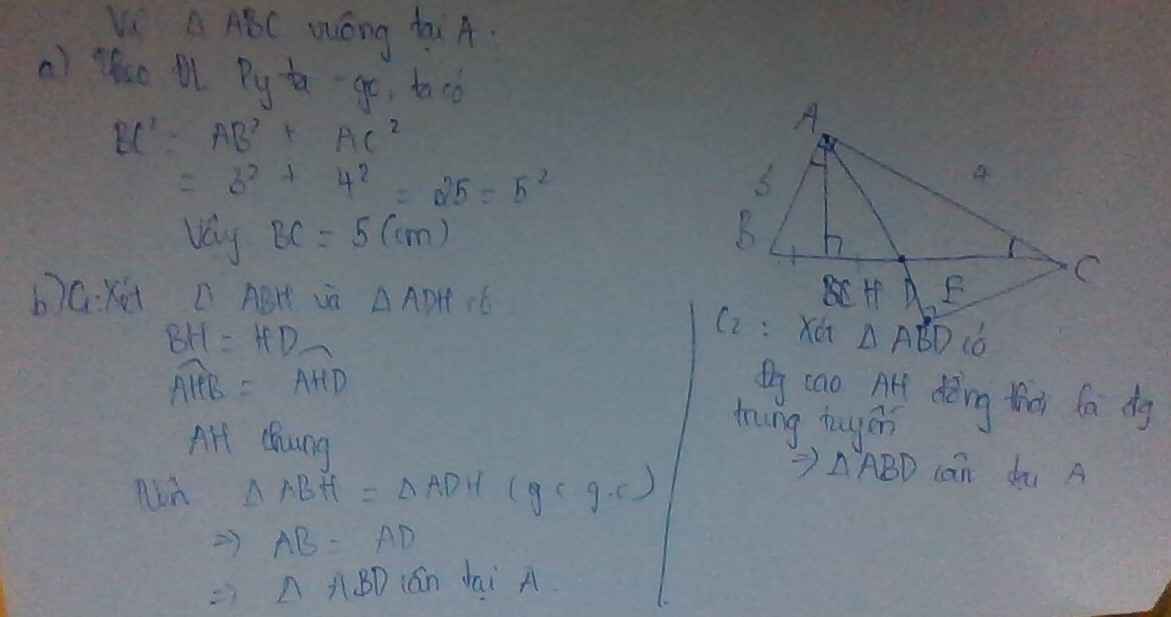

 giúp em với em cần gấp ạaa
giúp em với em cần gấp ạaa
Đặt \(M\left(x\right)=0\Rightarrow3.\left(2-x\right)+\left(x-2\right)^2=0\)
\(\Rightarrow-3.\left(x-2\right)+\left(x-2\right)^2=0\)
\(\Rightarrow\left(x-2\right).\left[\left(-3\right)+\left(x-2\right)\right]=0\\ \Rightarrow\left(x-2\right).\left(x-2-3\right)=0\\ \Rightarrow\left(x-2\right).\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x-5=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
Vậy \(M\left(x\right)\) có nghiệm là \(x=2,x=5\).
`M(x)=3.(2-x)+(x-2)^2`
Ta có :
`3.(2-x)+(x-2)^2=0`
`=>3.(2-x)+(2-x)^2=0`
`=>(2-x).(3+2-x)=0`
`=>(2-x).(5-x)=0`
\(\Rightarrow\left[{}\begin{matrix}2-x=0\\5-x=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)