DT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 11 2021
\(1,\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(-3\right)^2-4\left(-2\right)\left(-m+1\right)>0\\x_1+x_2=\dfrac{3}{-2}< 0\\x_1x_2=\dfrac{-m+1}{-2}>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}17-8m>0\\-m+1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{17}{8}\\m>1\end{matrix}\right.\Leftrightarrow1< m< \dfrac{17}{8}\)
\(2,\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(-4\right)^2-4\left(-3\right)\left(-2m+1\right)\ge0\\x_1+x_2=\dfrac{4}{-3}< 0\\x_1x_2=\dfrac{-2m+1}{-3}>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}28-24m\ge0\\-2m+1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{7}{6}\\m>\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}< m\le\dfrac{7}{6}\)
HH
0
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
ĐKXĐ: \(x\ge0\)
\(\left(x^2-x-m\right)\sqrt{x}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)
Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm
Do đó:
a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm
\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)
b. Để pt có 2 nghiệm pb
TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0
\(\Leftrightarrow m=0\)
TH2: (1) có 2 nghiệm trái dấu
\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)
\(\Rightarrow m\ge0\)
c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2021
Với \(x=0\) ko phải nghiệm
Với \(x\ne0\) chia 2 vế cho \(x^2\) ta được:
\(x^2+\dfrac{1}{x^2}+3x+\dfrac{3}{x}+m=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+3\left(x+\dfrac{1}{x}\right)+m-2=0\) (1)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow x^2-tx+1=0\) (2)
(2) có 2 nghiệm pb khi và chỉ khi:
\(\Delta=t^2-4>0\Rightarrow\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
Khi đó (1) trở thành:
\(t^2+3t+m-2=0\) (3)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (3) có 2 nghiệm pb thỏa mãn \(\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
(3) \(\Leftrightarrow t^2+3t-2=-m\)
Đặt \(f\left(t\right)=t^2+3t-2\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=8\)
Đồ thị hàm \(f\left(t\right)\):
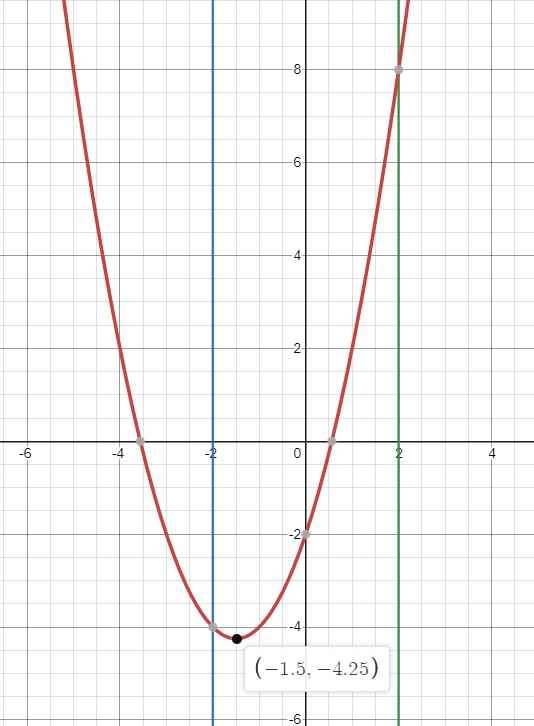
Từ đồ thị ta thấy \(y=-m\) cắt \(y=f\left(t\right)\) tại 2 điểm đều nằm ngoài \(\left[-2;2\right]\) khi và chỉ khi:
\(\left[{}\begin{matrix}-\dfrac{17}{4}< -m< -4\\-m>8\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4< m< \dfrac{17}{4}\\m< -8\end{matrix}\right.\)
26 tháng 7 2021
thầy cho em hỏi làm mấy dạng tìm điều kiện này thạo thì nên học qua tư liệu nào ? Thầy có thể cho e một số file chuyên đề về mấy dạng này đc không?
HP
16 tháng 2 2021
a, Phương trình có hai nghiệm trái dấu khi \(2\left(2m^2-3m-5\right)< 0\)
\(\Leftrightarrow\left(2m-5\right)\left(m+1\right)< 0\)
\(\Leftrightarrow-1< m< \dfrac{5}{2}\)
b, TH1: \(m^2-3m+2=0\Leftrightarrow\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\)
Phương trình đã cho có nghiệm duy nhất
TH2: \(m^2-3m+2\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m\ne2\end{matrix}\right.\)
Phương trình có hai nghiệm trái dấu khi \(-5\left(m^2-3m+2\right)< 0\)
\(\Leftrightarrow m^2-3m+2>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>2\\m< 1\end{matrix}\right.\)
Vậy \(m>2\) hoặc \(m< 1\)
TD
0
NT
0
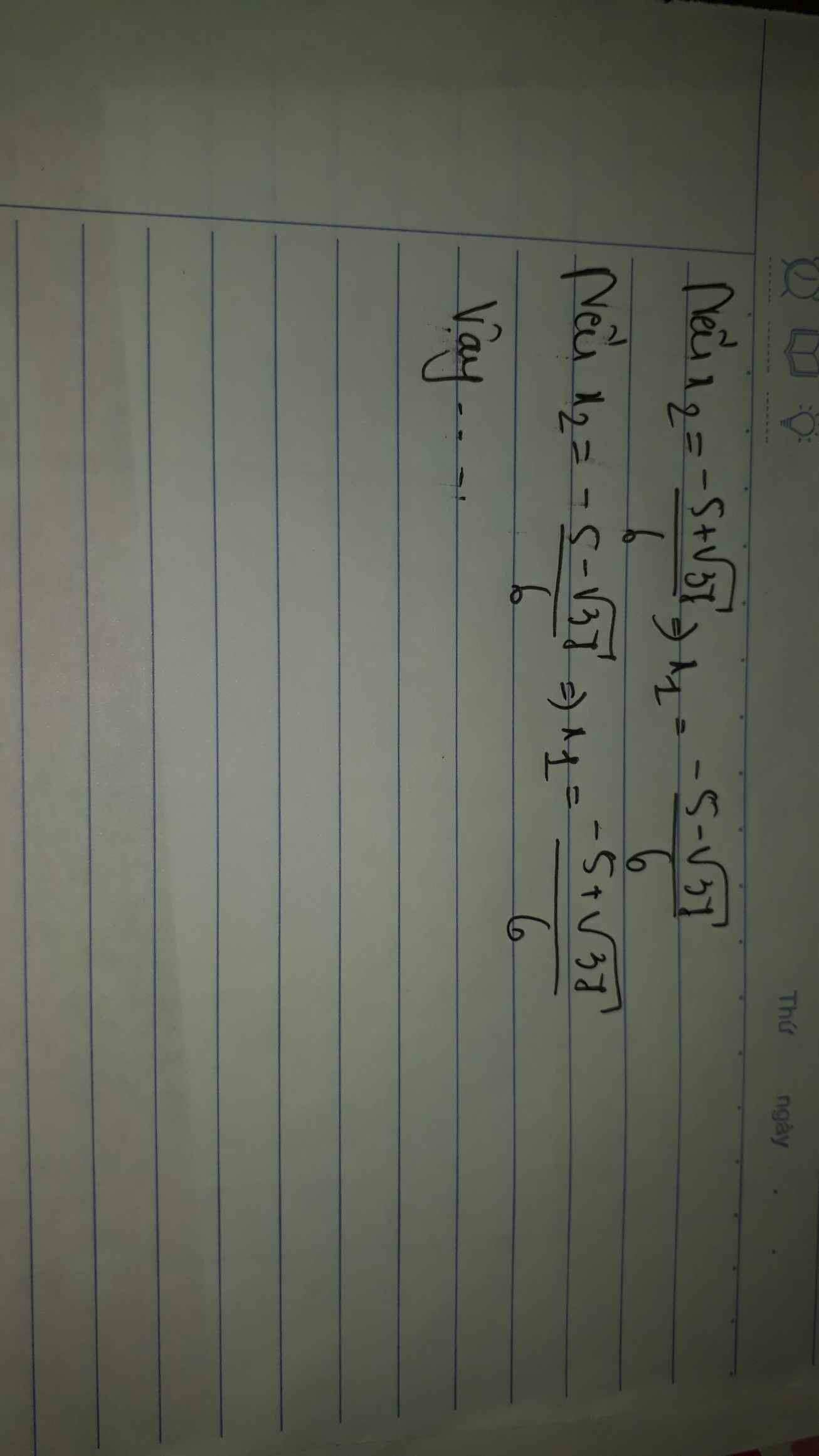
PT có 2 no âm phân biệt \(\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(-3\right)^2-4\left(-2\right)\left(-m+1\right)>0\\x_1+x_2=\dfrac{3}{-2}< 0\\x_1x_2=\dfrac{-m+1}{-2}>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}17-8m>0\\-m+1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{17}{8}\\m>1\end{matrix}\right.\Leftrightarrow1< m< \dfrac{17}{8}\)
Mình chưa hiểu ngay chỗ \(\dfrac{-m+1}{-2}\)> 0 ➜ -m+1<0 v á.