Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x2-4x+7 = 0 ⇔ x2 -4x + 4 + 3 = 0
⇔ (x-2)2+3=0 ⇔ (x-2)2=-3 (vô lí)
Vậy pt vô nghiệm
*Chứng minh phương trình \(x^2-4x+7=0\) vô nghiệm
Ta có: \(x^2-4x+7=0\)
\(\Leftrightarrow x^2-4x+4+3=0\)
\(\Leftrightarrow\left(x-2\right)^2+3=0\)
mà \(\left(x-2\right)^2+3\ge3>0\forall x\)
nên \(x\in\varnothing\)(đpcm)

Tìm xy biết xy+2x-5y=0( x, y thuộc Z)
\(\Rightarrow x(y+2)-5(y+2)=-10\)
\(\Rightarrow(x-5)(y+2)=-10\)
Vì \(x,y\in Z\Rightarrow x-5,y+2\in Z\)
Ta có bảng sau:
| x-5 | 1 | -1 | -2 | -5 | 2 | 5 | 10 | -10 |
| y+2 | -10 | 10 | 5 | 2 | -5 | -2 | -1 | 1 |
| x | 6 | 4 | 3 | 0 | 7 | 10 | 15 | -5 |
| y | -12 | 8 | 3 | 0 | -7 | -4 | -3 | -1 |
Chúc bạn học tốt!

Bài 1:
a) 2(x + 1) = 3 + 2x
⇔ 2x + 2 = 3 + 2x
⇔ 0x = 1 (vô lí)
Vậy phương trình vô nghiệm.
b) 2(1 - 1,5x) + 3x = 0
⇔ 2 - 3x + 3x = 0
⇔ 2 = 0 (vô lí)
Vậy phương trình vô nghiệm.
c) |x| = - 1 (vô lí vì |x| ≥ 0)
Vậy phương trình vô nghiệm.
d) x2 + 1 = 0
⇔ x2 = -1 (vô lí vì x2 ≥ 0)
Vậy phương trình vô nghiệm.
Bài 2:
a) 3x - 11 = 0
⇔ 3x = 11
⇔ x = \(\frac{11}{3}\) \(\approx\) 3,67
Vậy...
b) 12 + 7x = 0
⇔ 7x = -12
⇔ x = \(\frac{-12}{7}\) \(\approx\) -1,71
Vậy...
c) 10 - 4x = 2x - 3
⇔ 6x = 13
⇔ x = \(\frac{13}{6}\approx\) 2,17
Vậy...

3/(x^2-13x+40)+2/(x^2-8x+15)+1/(x^2-5x+6)+6/5+0
3/(x-8)(x-5)+2/(x-5)(x-3)+1/(x-3)(x-2)+6/5=0
1/(x-8)-1/(x-5)+1/(x-5)-1/(x-3)+1/(x-3)-1/(x-2)+6/5=0
1/(x-8)-1/(x-2)+6/5=0
ban tu giai tiep nhan
m^2x+2x=5-3mx
m^2x+3mx+2x=5
x(m^2+3m+2)=5
khi 0x=5 thi pt vo nghiem
m^2+3m+2=0
(m+1)(m+2)=0
m=-1 hoac m=-2

Bài 2:
a) Ta có: \(2\left(x+1\right)=3+2x\)
\(\Leftrightarrow2x+2-3-2x=0\)
\(\Leftrightarrow-1< 0\)
Do đó: Phương trình \(2\left(x+1\right)=3+2x\) vô nghiệm
b) Ta có: \(\left|x\right|\ge0\forall x\)
\(\Rightarrow\left|x\right|+1\ge1>0\forall x\)
Do đó: Phương trình |x|+1=0 vô nghiệm
c) Ta có: \(x^2\ge0\forall x\)
\(\Rightarrow x^2+1\ge1>0\forall x\)
Do đó: Phương trình x2+1=0 vô nghiệm
Bài 3:
a) Thay x=-2 vào phương trình \(2x+k=x-1\), ta được
\(2\cdot\left(-2\right)+k=-2-1\)
\(\Leftrightarrow-4+k=-3\)
hay k=1
Vậy: Khi k=1 thì phương trình \(2x+k=x-1\) có nghiệm là x=-2
b) Thay x=2 vào phương trình \(\left(2x+1\right)\left(9x+2k\right)-5\left(x+2\right)=40\), ta được
\(\left(2\cdot2+1\right)\left(9\cdot2+2k\right)-5\left(2+2\right)=40\)
\(\Leftrightarrow5\cdot\left(18+2k\right)-20=40\)
\(\Leftrightarrow5\left(18+2k\right)=60\)
\(\Leftrightarrow18+2k=12\)
\(\Leftrightarrow2k=-6\)
hay k=-3
Vậy: Khi k=-3 thì phương trình \(\left(2x+1\right)\left(9x+2k\right)-5\left(x+2\right)=40\) có nghiệm là x=2
Bài 4:
Ta có: (x-1)(2x-1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\2x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\frac{1}{2}\end{matrix}\right.\)
Vậy: Tập nghiệm \(S_1=\left\{1;\frac{1}{2}\right\}\)
Gọi S2 là tập nghiệm của phương trình \(mx^2-\left(m+1\right)x+1=0\)
Để hai phương trình (x-1)(2x-1)=0 và \(mx^2-\left(m+1\right)x+1=0\) là hai phương trình tương đương thì hai phương trình này phải có chung tập nghiệm
⇔S1=S2
hay \(S_2=\left\{1;\frac{1}{2}\right\}\)
Thay x=1 vào phương trình \(mx^2-\left(m+1\right)x+1=0\), ta được
\(m\cdot1^2-\left(m+1\right)\cdot1+1=0\)
\(\Leftrightarrow m-\left(m+1\right)=-1\)
\(\Leftrightarrow m-m-1=-1\)
hay -1=-1
Thay \(x=\frac{1}{2}\) vào phương trình \(mx^2-\left(m+1\right)x+1=0\), ta được
\(m\cdot\left(\frac{1}{2}\right)^2-\left(m+1\right)\cdot\frac{1}{2}+1=0\)
\(\Leftrightarrow\frac{1}{4}m-\left(m+1\right)\cdot\frac{1}{2}=-1\)
\(\Leftrightarrow\frac{1}{4}m-\frac{1}{2}m-\frac{1}{2}=-1\)
\(\Leftrightarrow\frac{-1}{4}m=-\frac{1}{2}\)
hay 1\(m=2\)
Vậy: Khi m=2 thì hai phương trình \(mx^2-\left(m+1\right)x+1=0\) và (x-1)(2x-1)=0 là hai phương trình tương đương
Bài 5:
1:
a) Ta có: 7x+12=0
⇔7x=-12
hay \(x=\frac{-12}{7}\)
Vậy: \(x=\frac{-12}{7}\)
b) Ta có: -2x+14=0
⇔-2x=-14
hay x=7
Vậy: x=7
2)
a) Ta có: 3x+1=7x-11
⇔3x+1-7x+11=0
⇔-4x+12=0
⇔-4x=-12
hay x=3
Vậy: x=3
b) Ta có: 2x+x+12=0
⇔3x+12=0
⇔3x=-12
hay x=-4
Vậy: x=-4
c) Ta có: x-5=3-x
⇔x-5-3+x=0
⇔2x-8=0
⇔2x=8
hay x=4
Vậy: x=4
d) Ta có: 7-3x=9-x
⇔7-3x-9+x=0
⇔-2x-2=0
⇔-2x=2
hay x=-1
Vậy: x=-1

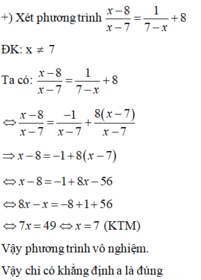
\(x^2-8x+17=0\)
\(\Leftrightarrow\)\(x^2-8x+16+1=0\)
\(\Leftrightarrow\)\(\left(x-4\right)^2+1=0\)
Ta thấy \(\left(x-4\right)^2\ge0\)\(\Rightarrow\)\(\left(x-4\right)^2+1\ge1\)
Vậy pt vô nghiệm