Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

Đáp án B
Đồ thị hàm số (C) có đường tiệm cận đứng là x = 2, tiệm cận ngang là y = 1.
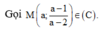
Tổng khoảng cách từ M đến hai đường tiệm cận bằng 2
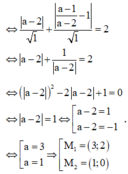

Đáp án B
Gọi M a; a + 2 a − 2 thuộc đồ thị hàm số
d ( M;TCD ) = a − 2
d ( M;TCN ) = 4 a − 2
Tổng khoảng cách= a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4
Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0 do hoành độ dương nên a=4
Vậy M(4;3)

Đáp án B
Gọi M a; a + 2 a − 2 thuộc đồ thị hàm số
d ( M;TCD ) = a − 2
d ( M;TCN ) = 4 a − 2
Tổng khoảng cách = a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4
Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0 do hoành độ dương nên a=4
Vậy M(4;3)
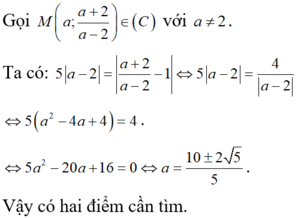
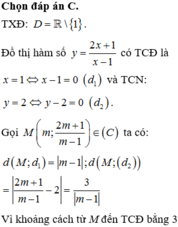



M m ; 2 m + 1 m - 1 ∈ C m ≠ 1
Tiệm cận đứng x = 1 và tiệm cận ngang y = 2
Yêu cầu bài toán
⇔ a - 1 = 3 2 a + 1 a - 2 - 2 ⇔ a = 4 ⇒ M 4 ; 3 a = - 2 ⇒ M - 2 ; 1
Đáp án C