Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có: x 2 − x + 1 20 có số hạng tổng quát là C 20 k x 2 − x k
Mặt khác x 2 − x k có số hạng tổng quát là C k i x 2 i . − x k − i = C k i x k + i . − 1 k − i
Do đó số hạng tổng quát của khai triển là C 20 k . C k i . x k + i − 1 k − i (với k ; i ∈ ℕ ; i ≤ k ≤ 20 )
Với k + i = 3 ⇒ i = 0 ; k = 3 i = 1 ; k = 2
Hệ số bằng C 20 3 . C 3 0 . − 1 3 + C 20 2 . C 2 1 . − 1 1 = − 1520

Đáp án A
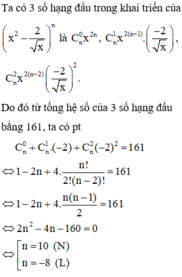
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
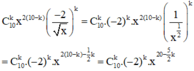
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho
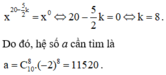

Đáp án A
Phương pháp: Sử dụng khai triển nhị thức Newton:
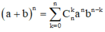
Cách giải:
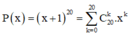
Để tìm hệ số của x 7 ta cho k = 7, khi đó hệ số của x 7 là C 20 7

Đáp án là B
Ta có: x + 2 x 6 = ∑ k = 0 6 C 6 k 2 k x 6 − 3 2 k
Do đó số hạng chứa x 3 trong khai triển ứng với k thỏa mãn: 6 − 3 2 k = 3 ⇔ k = 2
Hệ số của x 3 trong khai triển là: C 6 2 2 2 = 60


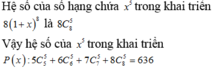



Đáp án B
Ta có 1 − 2 x 10 = ∑ k = 0 10 C 10 k 1 10 − k − 2 x k = ∑ k = 0 10 C 10 k − 2 k x k
Số hạng chứa x 3 ⇔ k = 3 ⇒ a 3 = C 10 3 − 2 3 x 3 = − 960 x 3