Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: 2|x + 2| \(\ge\)0 \(\forall\)x
=> 2|x + 2| + 15 \(\ge\)15 \(\forall\)x
Hay A \(\ge\)15 \(\forall\)x
Dấu "=" xảy ra <=>x + 2 = 0 <=> x = -2
Vậy Min A = 15 tại x = -2
b) Ta có: 2(x + 5)4 \(\ge\)0 \(\forall\)x
3|x + y + 2| \(\ge\)0 \(\forall\)x;y
=> 20 - 2(x + 5)4 - 3|x + y + 2| \(\le\)20 \(\forall\)x;y
Hay B \(\le\)20 \(\forall\)x;y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+5=0\\x+y+2=0\end{cases}}\) <=> \(\hept{\begin{cases}x=-5\\y=-2-x\end{cases}}\) <=> \(\hept{\begin{cases}x=-5\\y=-2-\left(-5\right)=3\end{cases}}\)
Vậy Max B = 20 tại x = -5 và y = 3

\(\dfrac{x}{6}=\dfrac{7}{4}\Rightarrow x=\dfrac{6\cdot7}{4}=\dfrac{21}{2}\\ \dfrac{3}{x}=\dfrac{21}{17}\Rightarrow x=\dfrac{3\cdot17}{21}=\dfrac{17}{7}\)

Gọi số hoa của 3 bạn lần lượt là x, y , z
Vì x,y,z TLT vớ 4,5,6
=> x/4=y/5=z/6=k
Theo t/c dãy tỉ số bằng nhau :
k= x+y+z/ 4+5+6 = 75/15=5
=> x= 5.4=20
y= 5. 5 = 25
z= 5.6=30
Vậy ..
Gọi số hoa 3 bạn hái được lần lượt là a,b,c \(\left(a,b,c\inℕ^∗\right)\)
Theo đề bài ra,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{75}{15}=6\)
\(\Rightarrow\hept{\begin{cases}a=6.4=24\\b=6.5=30\\c=6.6=36\end{cases}}\)
Vậy ....

b: Ta có: \(47\dfrac{1}{9}:\left(-\dfrac{5}{2}\right)-27\dfrac{1}{9}:\left(-\dfrac{5}{2}\right)\)
\(=\left(47+\dfrac{1}{9}\right)\cdot\dfrac{-2}{5}-\left(27+\dfrac{1}{9}\right)\cdot\dfrac{-2}{5}\)
\(=20\cdot\dfrac{-2}{5}\)
=-8

có gì ko hiểu bạn hỏi nhé
\(|2x+1|-|x-1|=3x\left(1\right)\)
Ta có:
\(2x+1=0\Leftrightarrow x=\frac{-1}{2}\)
\(x-1=0\Leftrightarrow x=1\)
Lập bảng xét dấu :
2x+1 x-1 -1/2 1 -0 0 0 - - - + + + +
+) Với \(x< \frac{-1}{2}\Rightarrow\hept{\begin{cases}2x+1< 0\\x-1< 0\end{cases}\Rightarrow}\hept{\begin{cases}|2x+1|=-2x-1\\|x-1|=1-x\end{cases}\left(2\right)}\)
Thay (2) vào (1) ta được :
\(\left(-2x-1\right)-\left(1-x\right)=3x\)
\(-2x-1-1+x=3x\)
\(-2x+x-3x=1+1\)
\(-4x=2\)
\(x=\frac{-1}{2}\)( loại )
+) Với \(\frac{-1}{2}\le x< 1\Rightarrow\hept{\begin{cases}2x+1>0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|2x+1|=2x+1\\|x-1|=1-x\end{cases}\left(3\right)}}\)
Thay (3) vào (1) ta được :
\(\left(2x+1\right)-\left(1-x\right)=3x\)
\(2x+1-1+x=3x\)
\(3x=3x\)( luôn đúng chọn )
+) Với \(x\ge1\Rightarrow\hept{\begin{cases}2x+1>0\\x-1>0\end{cases}\Rightarrow\hept{\begin{cases}|2x+1|=2x+1\\|x-1|=x-1\end{cases}\left(4\right)}}\)
Thay (4) vào (1) ta được :
\(\left(2x+1\right)-\left(x-1\right)=3x\)
\(2x+1-x+1=3x\)
\(2x-x-3x=-1-1\)
\(-2x=-2\)
\(x=1\)( chọn )
Vậy \(\frac{-1}{2}\le x\le1\)
\(\left|2x+1\right|-\left|x-1\right|=3x\Rightarrow\left|2x+1-1+x\right|\ge3x\)
\(\Leftrightarrow\left|3x\right|\ge3x\Rightarrow x\in\left\{x\inℤ|x\le0\right\}\)

\(A=\dfrac{3}{2\cdot2}=\dfrac{3}{4}\\ A=\dfrac{3}{2\cdot5}=\dfrac{3}{10}\\ A=\dfrac{3}{2\cdot3}=\dfrac{1}{2}\)


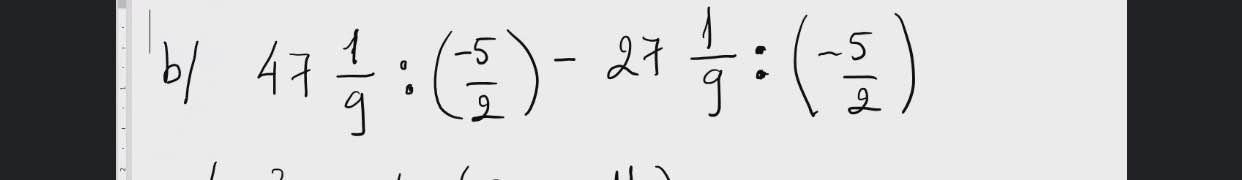

Cho bạn biết nhé : bạn thiếu điều kiện òi
Úi chít, mik quên.
Cho hàm số: y=f(x)=ax