HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
27 tháng 1 2016
Gọi hai số cần tìm là a và b
Tổng hai số bằng 7 nên ta có pt: a+b=7 <=>a=7-b
Tổng nghịch đảo của chúng bằng 7/12 nên ta có pt:
\(\frac{1}{a}+\frac{1}{b}=\frac{7}{12}\Leftrightarrow\frac{a+b}{ab}=\frac{7}{12}\Leftrightarrow\frac{7}{ab}=\frac{7}{12}\Leftrightarrow ab=12\)(2)
Thay a=7-b vào (2) ta đc: b(7-b)=12
<=>-b2+7b-12=0
<=>b=4 hoặc b=3
Suy ra a=3 hoặc a=4
Vậy 2 số cần tìm là 3 và 4
CP
0
17 tháng 3 2023
Gọihai số cần tìm lần lượt là a,b
Theo đề, ta có: a+b=84 và a=6b+7
=>a+b=84 và a-6b=7
=>a=73 và b=11
20 tháng 3 2023
Gọi hai số cần tìm lần lượt là a,b
Theo đề, ta có: a+b=84 và a=6b+7
=>a+b=84 và a-6b=7
=>a=73 và b=11
PT
1
CM
26 tháng 4 2017
Vì hai số có tổng bằng 10 và tích bằng -10 nên nó là nghiệm của phương trình: x 2 – 10x – 10 = 0
Ta có: ∆ ' = - 5 2 – 1.(-10) = 25 + 10 = 35 > 0
∆ ' = 35
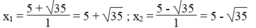
Vậy hai số đó là 5 + 35 và 5 - 35
HM
7
PA
14 tháng 5 2016
Tổng số phần bằng nhau:
\(1+2=3\)
Số thứ nhất là:
\(12\div3\times1=4\)
Số thứ hai là:
\(12-4=8\)
Chúc bạn học tốt
14 tháng 5 2016
Số thứ nhất: |___|
Số thứ hai: |___|___|
Tổng số phần bằng nhau là: 1+2=3 (phần)
Số thứ nhất là: 12.1:3=4
Số thứ hai là: 12.2:3=8
DT
0
SG
1
8 tháng 5 2017
tìm 2 số có : tổng = 10 và tích = -10
2 số đó là nghiệm của phương trình
x2- 10x - 10 = 0
\(\Delta\) = (-10)2-4.1.(-10) = 100 + 40 = 140 > 0
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
x1= \(\dfrac{10+\sqrt{140}}{2}\) =5 + \(\sqrt{35}\)
x2=\(\dfrac{10-\sqrt{140}}{2}\) =5 - \(\sqrt{35}\)
vậy 2 số đó là :5 + \(\sqrt{35}\) và 5 - \(\sqrt{35}\)
TM
0
Gọi 2 số đó là a và b ( \(a,b\ne0\) )
Theo đề bài ta có hệ:
\(\left\{{}\begin{matrix}a+b=7\\\frac{1}{a}+\frac{1}{b}=\frac{7}{12}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=7-a\\\frac{1}{a}+\frac{1}{7-a}=\frac{7}{12}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3\\b=7-a\end{matrix}\right.\\\left\{{}\begin{matrix}a=4\\b=7-a\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3\\b=4\end{matrix}\right.\\\left\{{}\begin{matrix}a=4\\b=3\end{matrix}\right.\end{matrix}\right.\)
Vậy....