TG
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
D
1
A
2
11 tháng 6 2021
\(A=\)\(\sqrt{x+2\left(1+\sqrt{x+1}\right)}+\sqrt{x+2\left(1-\sqrt{x+1}\right)}\) (đk: \(x\ge-1\))
\(=\sqrt{\left(x+1\right)+2\sqrt{x+1}+1}+\sqrt{\left(x+1\right)-2\sqrt{x+1}+1}\)
\(=\sqrt{\left(\sqrt{x+1}+1\right)^2}+\sqrt{\left(\sqrt{x+1}-1\right)^2}\)
\(=\sqrt{x+1}+1+\left|\sqrt{x+1}-1\right|\)
\(=\left[{}\begin{matrix}\sqrt{x+1}+1+\sqrt{x+1}-1;\sqrt{x+1}\ge1\\\sqrt{x+1}+1-\left(\sqrt{x+1}-1\right);\sqrt{x+1}< 1\end{matrix}\right.\)
\(=\left[{}\begin{matrix}2\sqrt{x+1};x\ge0\\2;-1\le x< 0\end{matrix}\right.\)
Có \(2\sqrt{x+1}\ge2\) tại \(x\ge0\)
\(\Rightarrow\min\limits_{x\ge0}A=2\)
Dấu = xảy ra <=> x=0 mà tại \(-1\le x< 0\) thì A=2
Vậy giá trị nhỏ nhất của biểu thức là 2 tại x=0 hoặc \(-1\le x< 0\)
(Ủa đề zì kì)
11 tháng 6 2021
\(ĐKXĐ:x\ge-1\)
Đặt \(A=\sqrt{x+2\left(1+\sqrt{x+1}\right)}+\sqrt{x+2\left(1-\sqrt{x+1}\right)}\)
\(=\sqrt{x+1+2\sqrt{x+1}+1}+\sqrt{x+1-2\sqrt{x+1}+1}\)
\(=\sqrt{\left(\sqrt{x+1}+1\right)^2}+\sqrt{\left(\sqrt{x+1}-1\right)^2}\)
\(=\left|\sqrt{x+1}+1\right|+\left|\sqrt{x+1}-1\right|\)
\(=\left|\sqrt{x+1}+1\right|+\left|1-\sqrt{x+1}\right|\)
\(\ge\left|\sqrt{x+1}+1+1-\sqrt{x+1}\right|=2\)
Dấu "=" xảy ra khi \(\left(\sqrt{x+1}+1\right)\left(1-\sqrt{x+1}\right)\ge0\)
\(\Leftrightarrow1-\sqrt{x+1}\ge0\)
\(\Leftrightarrow\sqrt{x+1}\le1\)
\(\Leftrightarrow x\le0\). Mà \(x\ge-1\) Nên \(-1\le x\le0\)
Vậy Min \(A=2\) khi \(-1\le x\le0\)
S
29 tháng 12 2020
\(ĐKXĐ:\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
\(P\left(x\right)=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(P\left(x\right)=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(P\left(x\right)=x-\sqrt{x}-2\sqrt{x}-2+2\sqrt{x}+2\)
\(P\left(x\right)=x-\sqrt{x}\)
Ta có : \(\dfrac{P\left(x\right)}{2020\sqrt{x}}=\dfrac{x-\sqrt{x}}{2020\sqrt{x}}=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2020\sqrt{x}}=\dfrac{\sqrt{x}-1}{2020}\)
Để \(\dfrac{P\left(x\right)}{2020\sqrt{x}}min\Leftrightarrow\dfrac{\sqrt{x}-1}{2020}min\Leftrightarrow\sqrt{x}-1\) min (vì 2020 > 0)
Lại có : \(\sqrt{x}-1\ge-1\forall x\)
Dấu "=" xảy ra <=> x = 0
Vậy Min\(\dfrac{P\left(x\right)}{2020\sqrt{x}}=\dfrac{-1}{2020}\Leftrightarrow x=0\)
KV
17 tháng 3 2019
\(F=\sqrt{x\left(x+1\right)\left(x+2\right)\left(x+3\right)+5}=\sqrt{\left(x^2+3x\right)\left(x^2+3x+2\right)+5}\) ( * )
*Đặt \(t=x^2+3x\)Ta có :
( * ) \(=\sqrt{t.\left(t+2\right)+5}=\sqrt{\left(t+1\right)^2+4}\)
( * ) Đạt GTNN của F khi bằng 2 khi \(t+1=0\) hay \(t=-1\)
Vậy \(^{minF=2\Leftrightarrow x=\frac{-3\pm\sqrt{5}}{2}}\)
25 tháng 8 2021
a: Ta có: \(\sqrt{x}\left(\sqrt{x}-3\right)-5\left(\sqrt{x}+3\right)\)
\(=x-3\sqrt{x}-5\sqrt{x}-15\)
\(=x-8\sqrt{x}-15\)
b: Ta có: \(3\left(\sqrt{x}+2\right)+\left(\sqrt{x}+3\right)\left(2-\sqrt{x}\right)\)
\(=3\sqrt{x}+6+2\sqrt{x}-x+6-3\sqrt{x}\)
\(=-x+2\sqrt{x}+12\)
c: Ta có: \(\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)-5\left(\sqrt{x}-1\right)\)
\(=x-9-5\sqrt{x}+5\)
\(=x-5\sqrt{x}-4\)
d: Ta có: \(3\left(\sqrt{x}-2\right)-\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
\(=3\sqrt{x}-6-x+1\)
\(=-x+3\sqrt{x}-5\)
TV
2
23 tháng 9 2018
Ta có: x(x+1)(x+2)(x+3)+5
= x(x+3)(x+1)(x+2)+5 = (x2 +3x)(x2 +3x +2)+5 = (x2 +3x +1 -1)(x2 +3x +1 +1) +5
= (x2 +3x +1)2 -1 +5 = (x2 +3x +1)2 +4
Vì (x2 +3x +1)2 ≥0 (∀x) nên (x2 +3x +1) +4 ≥4
⇒ C ≥ √4 ⇒ C ≥ 2
⇒ C đạt GTNN bằng 2 ⇔ (x2 +3x +1)2 =0
Bạn làm tiếp nha......
23 tháng 9 2018
Phan Văn KhởiPhùng Khánh LinNguyễn Thị Ngọc ThơhHoàng Ngọc Anh giup mk voi
W
2
BA
1 tháng 12 2019
Đặt \(F=\sqrt{x\left(x+1\right)\left(x+2\right)\left(x+3\right)+5}\)
\(=\sqrt{\left(x^2+3x\right)\left(x^2+3x+2\right)+5}\)
# đặt \(t=x^2+3x\) ta có
\(=\sqrt{t\cdot\left(t+2\right)+5}=\sqrt{\left(t+1\right)^2+4}\)
# đạt giá trị nhỏ nhất của F=2 khi t+1=0 hay t=-1
Vậy \(F_{min}=2\) khi \(x=\frac{-3\pm\sqrt{5}}{2}\)
DH
1 tháng 12 2019
Ta có: \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+5=\left(x^2+3x\right)\left(x^2+3x+2\right)+5\)
\(=\left(x^2+3x+1-1\right)\left(x^2+3x+1+1\right)+5=\left(x^2+3x+1\right)^2-1^2+5\)
\(=\left(x^2+3x+1\right)^2+4\ge4\)
Dấu "=" xảy ra khi \(\Leftrightarrow x^2+3x+1=0\)
\(\Leftrightarrow4x^2+12x+4=0\)
\(\Leftrightarrow\left(2x+3\right)^2=5\)
\(\Leftrightarrow x=\frac{-3\pm\sqrt{5}}{2}\)
Vậy: \(GTNN\) của biểu thức là \(\sqrt{4}=2\)
NH
1
25 tháng 6 2023
C=|x-2021|+|1-x|>=|x-2021+1-x|=2020
Dấu = xảy ra khi 1<=x<=2021
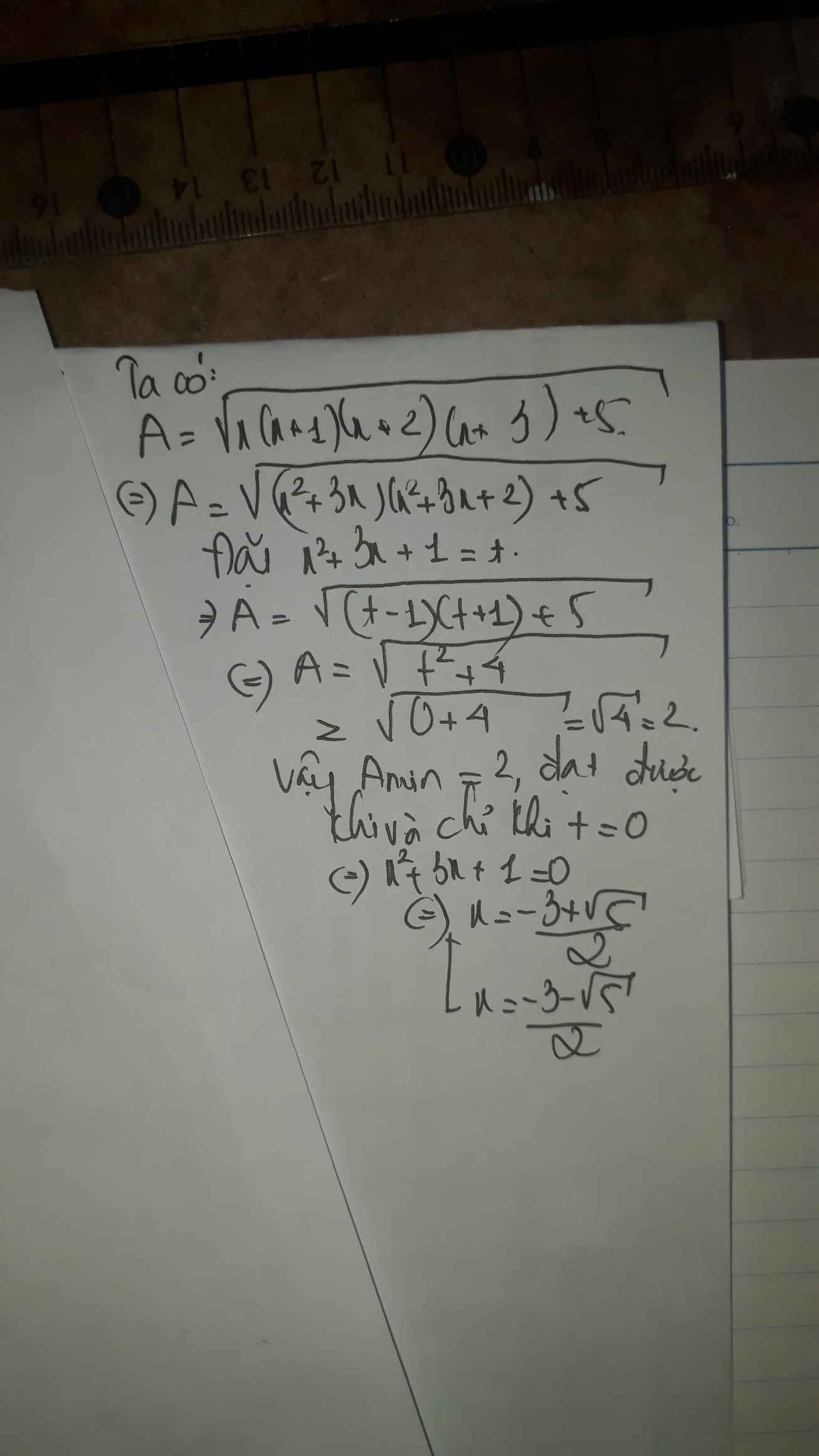
Đặt \(F=\sqrt{x\left(x+1\right)\left(x+2\right)\left(x+3\right)+5}\)
\(=\sqrt{\left(x^2+3x\right)\left(x^2+3x+2\right)+5}\left(#\right)\)
# đặt \(t=x^2+3x\) ta có
\(\left(#\right)=\sqrt{t\cdot\left(t+2\right)+5}=\sqrt{\left(t+1\right)^2+4}\)
(#) đạt giá trị nhỏ nhất của F=2 khi t+1=0 hay t=-1
Vậy \(F_{min}=2\) khi \(x=\frac{-3\pm\sqrt{5}}{2}\)