
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LH
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
1

AH
Akai Haruma
Giáo viên
13 tháng 9 2021
Lời giải:
TXĐ: $[-1;1]$
$y'=\frac{1}{2\sqrt{x+1}}-\frac{1}{2\sqrt{1-x}}+\frac{x}{2}$
$y'=0\Leftrightarrow x=0$
$f(0)=2$;
$f(1)=f(-1)=\sqrt{2}+\frac{1}{4}$
Vậy $f_{\min}=2; f_{\max}=\frac{1}{4}+\sqrt{2}$

9 tháng 6 2016
(sinx)4+(cosx)2+ 1 =>sinx4+sinx2 +2 => (sinx2-1/2)+3/4 => (((((Min = 3/4)))))
=> sinx=1/2
TK
0


AH
Akai Haruma
Giáo viên
22 tháng 8 2021
Lời giải:
\(y'=\frac{5-x}{\sqrt{(x^2+5)^3}}=0\Leftrightarrow x=5\)
Lập bảng biến thiên với các chốt $x=-\infty, x=5; x=+\infty$ ta thấy hàm số có GTLN tại $x=5$
Đáp án D.
TM
1

NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
Đề là \(\dfrac{cos^2x}{3}+\dfrac{sinx}{3}+1\) hay \(cos^2\left(\dfrac{x}{3}\right)+sin\left(\dfrac{x}{3}\right)+1\) vậy nhỉ?
NH
5

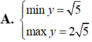
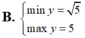
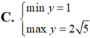
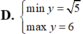
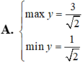
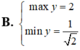
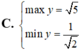
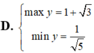
Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y = 2\sqrt{1-x^2} + x^2 \) trên miền xác định của nó, ta thực hiện các bước sau:
1. **Xác định miền xác định của hàm số**:
\[
1 - x^2 \geq 0 \implies -1 \leq x \leq 1
\]
Do đó, hàm số xác định trên khoảng \([-1, 1]\).
2. **Tính đạo hàm của hàm số**:
\[
y = 2\sqrt{1 - x^2} + x^2
\]
Đạo hàm của hàm số \( y \) là:
\[
y' = \frac{d}{dx} \left( 2\sqrt{1 - x^2} + x^2 \right)
\]
Áp dụng quy tắc đạo hàm:
\[
y' = 2 \cdot \frac{d}{dx} \left( \sqrt{1 - x^2} \right) + \frac{d}{dx} \left( x^2 \right)
\]
\[
= 2 \cdot \frac{1}{2\sqrt{1 - x^2}} \cdot (-2x) + 2x
\]
\[
= -\frac{2x}{\sqrt{1 - x^2}} + 2x
\]
\[
= 2x \left(1 - \frac{1}{\sqrt{1 - x^2}}\right)
\]
3. **Tìm các điểm cực trị**:
Giải phương trình \( y' = 0 \):
\[
-\frac{2x}{\sqrt{1 - x^2}} + 2x = 0
\]
\[
2x \left( 1 - \frac{1}{\sqrt{1 - x^2}} \right) = 0
\]
\[
2x = 0 \quad \text{hoặc} \quad 1 - \frac{1}{\sqrt{1 - x^2}} = 0
\]
\[
x = 0 \quad \text{hoặc} \quad \sqrt{1 - x^2} = 1
\]
\[
x = 0 \quad \text{hoặc} \quad 1 - x^2 = 1
\]
\[
x = 0 \quad \text{hoặc} \quad x^2 = 0
\]
\[
x = 0
\]
4. **Xét giá trị của hàm số tại các điểm biên và điểm cực trị**:
\[
y(-1) = 2\sqrt{1 - (-1)^2} + (-1)^2 = 2\sqrt{0} + 1 = 1
\]
\[
y(1) = 2\sqrt{1 - 1^2} + 1^2 = 2\sqrt{0} + 1 = 1
\]
\[
y(0) = 2\sqrt{1 - 0^2} + 0^2 = 2\sqrt{1} + 0 = 2
\]
Vậy giá trị lớn nhất của hàm số trên khoảng \([-1, 1]\) là \( 2 \) và giá trị nhỏ nhất là \( 1 \).