
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(-x^2-y^2+xy+2x+2y=-\left[x^2-x\left(y+2\right)+\dfrac{1}{4}\left(y+2\right)^2\right]-\left(\dfrac{3}{4}y^2-3y+3\right)+4=-\left(x-\dfrac{1}{2}y-1\right)^2-\left(\dfrac{\sqrt{3}}{2}y-\sqrt{3}\right)^2+4\le4\)
\(max=4\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

E XIN LỖI CHỊ , NHƯNG E MỚI HỌC LỚP 6
THÌ GIÚP CHỊ KIỂU GÌ Ạ ???
THÔI THÌ CHÚC CHỊ SẼ CHỌN ĐC CÂU TRẢ LỜI ƯNG Ý VỚI MK NHÉ ! MỌI NGƯỜI GIÚP CHỊ NHA !
\(x-x^2+1\)
\(=-\left(x^2-x-1\right)\)
\(=-\left(x^2-2.x.\frac{1}{2}+\frac{1}{4}-\frac{5}{4}\right)\)
\(=-\left(\left(x-\frac{1}{2}\right)^2-\frac{5}{4}\right)\)
\(=\frac{5}{4}-\left(x-\frac{1}{2}\right)^2\le\frac{5}{4}\)
Max\(=\frac{5}{4}\Leftrightarrow x-\frac{1}{2}=0\Rightarrow x=\frac{1}{2}\)

Câu E bạn xem lại đề nha
F=\(-y^2+2y-6\)
\(=-\left(y^2-2y+6\right)\)
\(=-\left(y-1\right)^2-5\)
Vì \(-\left(y-1\right)^2\le0\forall y\)
\(\Rightarrow F\le-5\forall y\)
\(MaxF=-5\Leftrightarrow y=1\)
\(F=-y^2+2y-6=-\left(y^2-2y+1\right)-5=-\left(y-1\right)^2-5\le-5\forall y\in R\\ Vậy:max_F=-5\Leftrightarrow y=1\)


* Tìm GTNN :
Ta có :
\(D=\frac{4x-3}{x+1}=\frac{4x+4-7}{x+1}=\frac{4x+4}{x+1}-\frac{7}{x+1}=\frac{4\left(x+1\right)}{x+1}-\frac{7}{x+1}=4-\frac{7}{x+1}\)
Để D đạt GTNN thì \(\frac{7}{x+1}\) phải đạt GTLN hay \(x+1>0\) và đạt GTNN
\(\Rightarrow\)\(x+1=1\)
\(\Rightarrow\)\(x=0\)
Suy ra :
\(D=\frac{4x-3}{x+1}=\frac{4.0-3}{0+1}=\frac{0-3}{1}=\frac{-3}{1}=-3\)
Vậy \(D_{min}=-3\) khi \(x=0\)
Chúc bạn học tốt ~
\(* Tìm GTNN : Ta có : \(D=\frac{4x-3}{x+1}=\frac{4x+4-7}{x+1}=\frac{4x+4}{x+1}-\frac{7}{x+1}=\frac{4\left(x+1\right)}{x+1}-\frac{7}{x+1}=4-\frac{7}{x+1}\) Để D đạt GTNN thì \(\frac{7}{x+1}\) phải đạt GTLN hay \(x+1>0\) và đạt GTNN \(\Rightarrow\)\(x+1=1\) \(\Rightarrow\)\(x=0\) Suy ra : \(D=\frac{4x-3}{x+1}=\frac{4.0-3}{0+1}=\frac{0-3}{1}=\frac{-3}{1}=-3\) Vậy \(D_{min}=-3\) khi \(x=0\) Chúc bạn học tốt ~ \)

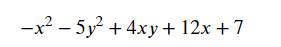
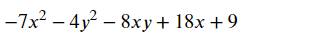 Tìm GTLN của biểu thức sau
Tìm GTLN của biểu thức sau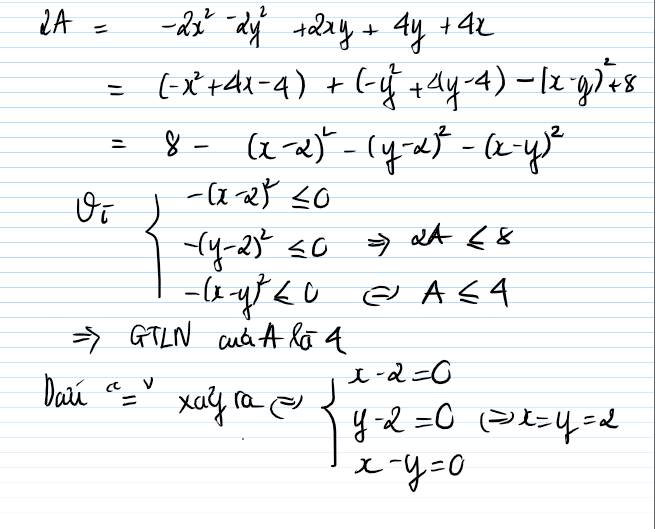
b: \(-7x^2-4y^2-8xy+18x+9\)
\(=\left(-4x^2-8xy-4y^2\right)+\left(-3x^2+18x-27\right)+36\)
\(=-4\left(x^2+2xy+y^2\right)-3\left(x^2-6x+9\right)+36\)
\(=-4\left(x+y\right)^2-3\left(x-3\right)^2+36< =36\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+y=0\\x-3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\)
a.
Đặt \(A=-x^2-5y^2+4xy+12x+7\)
\(=-\dfrac{1}{5}\left(4x^2-20xy+25y^2\right)-\dfrac{1}{5}\left(x^2-60x+900\right)+187\)
\(=-\dfrac{1}{5}\left(2x-5y\right)^2-\dfrac{1}{5}\left(x-30\right)^2+187\le187\)
\(A_{max}=187\) khi \(\left(x;y\right)=\left(30;12\right)\)