K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 12 2020
A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
19 tháng 12 2020
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2
AQ
1
12 tháng 1 2021
Ta có: \(P=2x-2xy-2x^2-y^2\)
\(P=-x^2-2xy-y^2-x^2+2x\)
\(P=-\left(x^2+2xy+y^2\right)-\left(x^2-2x+1\right)+1\)
\(P=-\left(x+y\right)^2-\left(x-1\right)^2+1\)
\(P=-\left[\left(x+y\right)^2+\left(x-1\right)^2\right]+1\le1\forall x;y\)
Vậy GTLN của P là 1 khi x=-1; y=1.
SS
17 tháng 8 2019
A= 2x^2 + y^2 - 2xy -2x+3
A= x^2-2xy + y^2 + x^2 - 2x+ 1 +2
A= (x-y)^2 + (x-1)^2 + 2
(x-y)^2> hoặc = 0 với mọi giá trị của x
(x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 + 2 > hoặc =2
=> A lớn hơn hoặc bằng 2
=> GTNN của A=2 tại x=y=1
20 tháng 9 2021
\(A=2x^2+y^2-2x+2xy+2y+3=y^2+2y\left(x+1\right)+\left(x+1\right)^2+\left(x^2-4x+4\right)-2=\left(y+x+1\right)^2+\left(x-2\right)^2-2\ge-2\)
\(minA=-2\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)
20 tháng 9 2021
\(P=x^3+2021xy+y^3\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+2021xy\)
\(=\left(\dfrac{2021}{3}\right)^3\)
\(=\dfrac{8254655261}{27}\)
OY
21 tháng 10 2021
a) \(2x^2+2x+1=0\)
\(\Rightarrow2x^2+2x=-1\)
\(\Rightarrow2x\left(x+1\right)=-1\)
⇒ Pt vô nghiệm
21 tháng 10 2021
a: \(2x^2+2x+1=0\)
\(\text{Δ}=2^2-4\cdot2\cdot1=4-8=-4< 0\)
Vì Δ<0 nên phương trình vô nghiệm
19 tháng 7 2017
\(2x^2\)+\(y^2\)-2xy+2x+2y+5=0
(\(x^2-2xy+y^2\))+2(x+y)+4+(\(x^2+1\))=0
(x-y)2 +2(x+y)+\(2^2\)+(\(x^2+1\))=0
(x-y+2)2 +(\(x^2+1\))=0
Với mọi x;y Thuộc R thì (x-y+2)2 >=0;\(x^2+1\)>0
suy ra (x-y+2)2 +\(x^2+1\)>0
Do đó không tìm được giá trị nào của x;y để 2x2 +\(y^2\)-2xy+2x+2y+5=0
Vậy không tìm đc giá trị nào của x;y thỏa mãn 2x2 +\(y^2\) -2xy+2x+2y+5=0
chúc bạn học tốt ạ
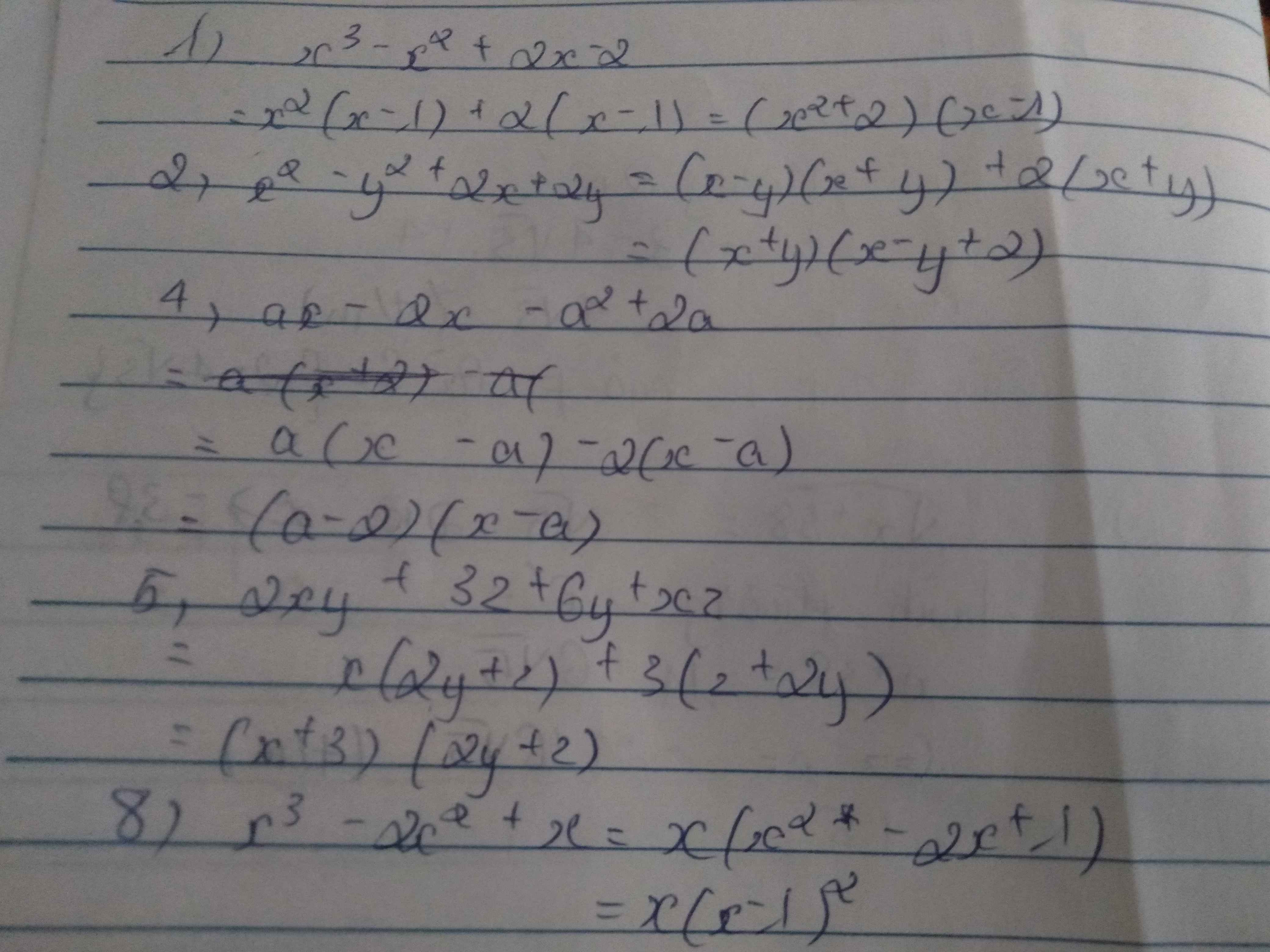
\(-2x^2-2xy-y^2+2x-2y-2=-\left[y^2+2y\left(x+1\right)+\left(x+1\right)^2\right]-\left(x^2-4x+4\right)+3=-\left(y+x+1\right)^2-\left(x-2\right)^2+3\le3\)
\(max=3\Leftrightarrow\) \(\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)