B
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 9 2021
\(\left|x-\dfrac{2}{3}\right|-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{3}\)
DN
1
3 tháng 1 2019
A=3x-17/4-x
=>(-1)A=17-3x/4-x
=>(-1)A=12-3x+5/4-x
=> (-1)A=3+(5/4-x)=>A=-3-(5/4-x)
Để A có GTNN=>-3-(5/4-x) có GTNN
=>5/4-x có GTLN
=>4-x có GTNN =>=>4-x=-5=>x=9
=>A=3.9-17/4-9
=>A=10/-5
=>A=-2
Vậy..........
HP
9 tháng 7 2016
\(b,B\left(x\right)=x\left(x-3\right)-2\left(x+5\right)=x^2-3x-2x-10=x^2-5x-10\)
\(=x^2-\frac{5}{2}x-\frac{5}{2}x+\frac{25}{4}-\frac{25}{4}-10=x\left(x-\frac{5}{2}\right)-\frac{5}{2}\left(x-\frac{5}{2}\right)-\frac{65}{4}\)
\(=\left(x-\frac{5}{2}\right)^2-\frac{65}{4}\)
Vì \(\left(x-\frac{5}{2}\right)^2\ge0=>\left(x-\frac{5}{2}\right)^2-\frac{65}{4}\ge-\frac{65}{4}\) (với mọi x)
Dấu "=" xảy ra \(< =>x-\frac{5}{2}=0< =>x=\frac{5}{2}\)
Vậy minB(x)=-65/4 khi x=5/2
\(c,C\left(x\right)=2x\left(x+1\right)-3x\left(x+1\right)=2x^2+2x-3x^2-3x=-x^2-x\)
\(=-\left(x^2+x\right)=-\left(x^2+x+1-1\right)=-\left(x^2+\frac{1}{2}x+\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}-1\right)\)
\(=-\left[x\left(x+\frac{1}{2}\right)+\frac{1}{2}\left(x+\frac{1}{2}\right)-\frac{1}{4}\right]=-\left[\left(x+\frac{1}{2}\right)^2-\frac{1}{4}\right]=\frac{1}{4}-\left(x+\frac{1}{2}\right)^2\)
Vì \(\left(x+\frac{1}{2}\right)^2\ge0=>\frac{1}{4}-\left(x+\frac{1}{2}\right)^2\le\frac{1}{4}\) (với mọi x)
Dấu "=" xảy ra \(< =>x+\frac{1}{2}=0< =>x=-\frac{1}{2}\)
Vậy maxC(x)=1/4 khi x=-1/2
HP
9 tháng 7 2016
\(A\left(x\right)=2x\left(x-1\right)-3\left(x-13\right)=2x^2-5x+39\)
\(=2\left(x^2-\frac{5}{2}x+\frac{39}{2}\right)=2\left(x^2-\frac{5}{4}x-\frac{5}{4}x+\frac{25}{16}-\frac{25}{16}+\frac{39}{2}\right)\)
\(=2\left[x\left(x-\frac{5}{4}\right)-\frac{5}{4}\left(x-\frac{5}{4}\right)\right]+\frac{287}{16}=2\left[\left(x-\frac{5}{4}\right)^2+\frac{287}{16}\right]=2\left(x-\frac{5}{4}\right)^2+\frac{287}{8}\)
Vì \(2\left(x-\frac{5}{4}\right)^2\ge0=>2\left(x-\frac{5}{4}\right)^2+\frac{287}{8}\ge\frac{287}{8}>0\) với mọi x
=>A(x) vô nghiệm (đpcm)
DT
1
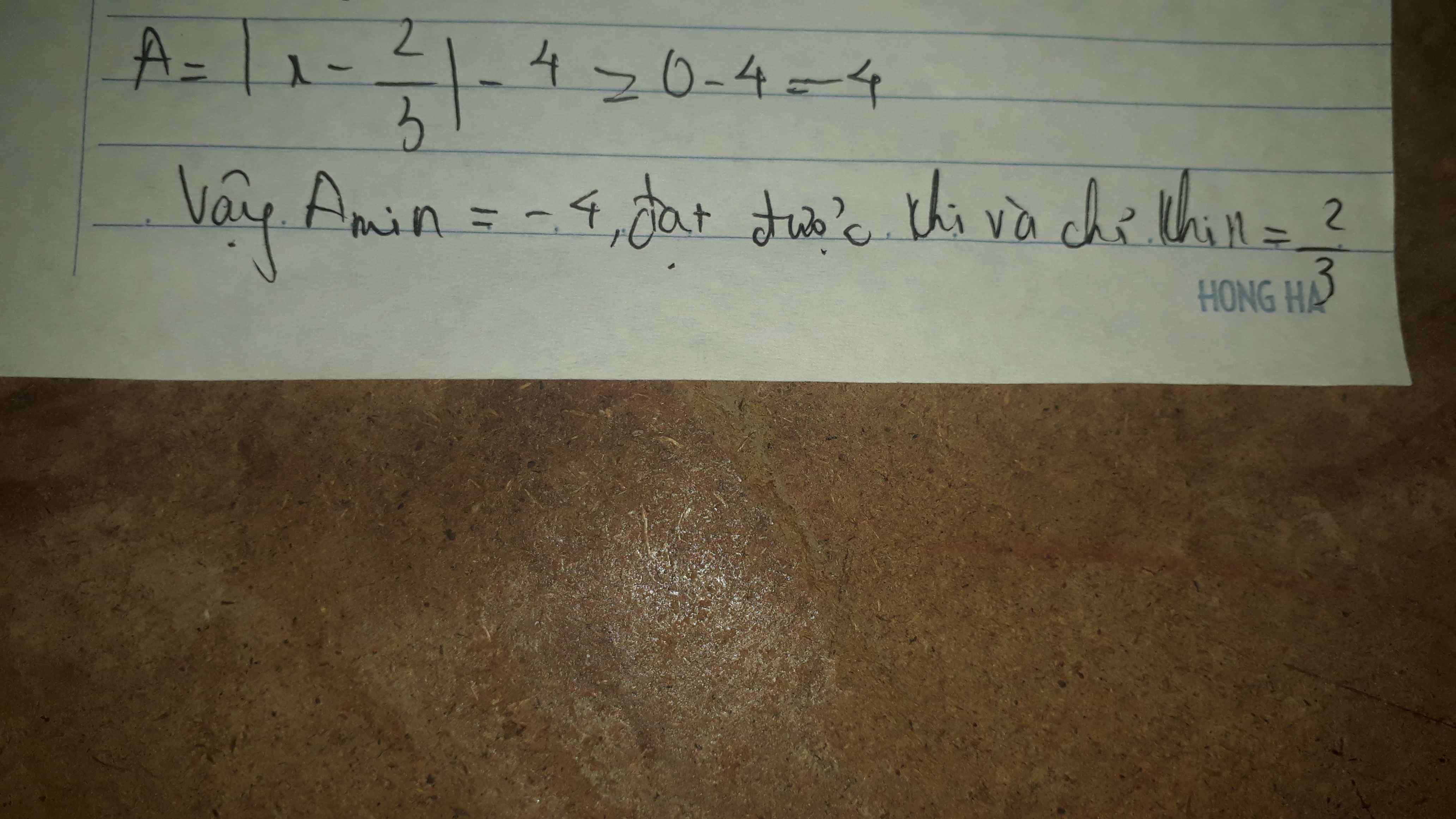
A=\(\frac{3.\left(x-2\right)-7}{x-2}=1-\frac{7}{x-2}\)
Để Amin \(\Rightarrow\)\(1-\frac{7}{x-2}\)min \(\Rightarrow\)\(\frac{-7}{x-2}\)min \(\Rightarrow x-2m\text{ax}\)
Xét x-2<0
A<1 \(\Rightarrow\)\(\frac{-7}{x-2}\) lớn nhất (1)
Xét x-2>0
A<1 \(\Rightarrow x-2nn\Rightarrow x-2=1\Rightarrow x=3\)(2)
từ 1 và 2 suy ra Min A=-4 khi x=3
\(\left|x-3\right|\ge0\)
\(\left|x+4\right|\ge0\)
\(\Rightarrow B\ge0\)
Dấu = xảy ra khi \(\orbr{\begin{cases}x-3=0\\x+4=0\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=-4\end{cases}}}\)
Vậy.....
Khuyển Dạ Xoa b) bạn sai rồi,thay x = 3 hoặc x = -4 xem có ra 0 hay không?
\(B=\left|x-3\right|+\left|x+4\right|=\left|3-x\right|+\left|x+4\right|\ge\left|3-x+x+4\right|=7\)
Dấu "=" xảy ra khi \(\left(3-x\right)\left(x+4\right)\ge0\Leftrightarrow\left(x-3\right)\left(x+4\right)\le0\Leftrightarrow-4\le x\le3\)
Vậy ...