Tìm giá trị nhỏ nhất của phân thức B = 2 x 2

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

28 tháng 7 2017

Tìm giá trị nhỏ nhất của phân thức B = 2 x 2 - 16 x + 41 x 2 - 8 x + 22

#Toán lớp 8

Cao Minh Tâm

28 tháng 7 2017

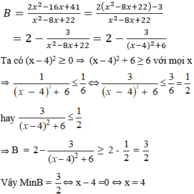
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án | Toán lớp 8

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

ThanhNghiem

21 tháng 10 2023

Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau
a) A= $\dfrac{-3}{x^2-5x+1}$

b) B=$\dfrac{2x^2+4x+4}{x^2}$

c) C= $\dfrac{2x^2-16x+41}{x^2-8x+22}$

#Toán lớp 8

Nguyễn Lê Phước Thịnh

21 tháng 10 2023

Đúng(2)

Xuyen Phan

20 tháng 7 2021

Bài 9 : tìm giá trị lớn nhất của biểu thức

A) -x^2-2x+3

B) -4x^2+4x-3

C) -x^2+6x-15

Bài 8 tìm giá trị nhỏ nhất của biểu thức

B)X² — 6x + 11

C. X² – x +1

D. X² – 12x + 2

#Toán lớp 8

Nguyễn Huy Tú

20 tháng 7 2021

a, $A=-x^2-2x+3=-\left(x^2+2x-3\right)=-\left(x^2+2x+1-4\right)$

$=-\left(x+1\right)^2+4\le4$

Dấu ''='' xảy ra khi x = -1

Vậy GTLN là 4 khi x = -1

b, $B=-4x^2+4x-3=-\left(4x^2-4x+3\right)=-\left(4x^2-4x+1+2\right)$

$=-\left(2x-1\right)^2-2\le-2$

Dấu ''='' xảy ra khi x = 1/2

Vậy GTLN B là -2 khi x = 1/2

c, $C=-x^2+6x-15=-\left(x^2-2x+15\right)=-\left(x^2-2x+1+14\right)$

$=-\left(x-1\right)^2-14\le-14$

Vâỵ GTLN C là -14 khi x = 1

Bài 8 :

b, $B=x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2$

Dấu ''='' xảy ra khi x = 3

Vậy GTNN B là 2 khi x = 3

c, $x^2-x+1=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}$

Dấu ''='' xảy ra khi x = 1/2

Vậy ...

c, $x^2-12x+2=x^2-12x+36-34=\left(x-6\right)^2-34\ge-34$

Dấu ''='' xảy ra khi x = 6

Vậy ...

Đúng(3)

Alexandra Alice

12 tháng 12 2016 - olm

1. Tìm các giá trị nguyên của x để các biểu thức sau có giá trị lớn nhấta. A=1/7-x b.B=27-2x/12-X2.Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nhỏ nhấta. A=1/x-3 b. B= 7-x/x-5 c. C= 5x-19/x-43.Tìm giá trị nhỏ nhất của các biếu thức saua. A=x^4+3x^2 +2 b. B=(x^4+5)^2 c. C=(x-1)^2+(y+2)^24.Tìm giá trị lớn nhất của các biểu thức saua. A=5-3(2x-1)^2 b.B=1/2(x-1)^2+3 c....

Đọc tiếp

#Toán lớp 8

Lê Thị Thanh Nhàn

26 tháng 8 2017 - olm

1, tìm giá trị nhỏ nhất của các biểu thức su

a,A=x^4-x^2+2*x+7

b,B=x^4-4*x^3+*x^2-20*x+22

#Toán lớp 8

Thánh Ca

27 tháng 8 2017

tuổi con HN là :

50 : ( 1 + 4 ) = 10 ( tuổi )

tuổi bố HN là :

50 - 10 = 40 ( tuổi )

hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi

ta có sơ đồ : bố : |----|----|----|

con : |----| hiệu 30 tuổi

tuổi con khi đó là :

30 : ( 3 - 1 ) = 15 ( tuổi )

số năm mà bố gấp 3 tuổi con là :

15 - 10 = 5 ( năm )

ĐS : 5 năm

mình nha

Đúng(0)

19.8A Trà My

27 tháng 12 2021

mình cần gấp mong mn giải cho mình nhanh

1. tìm giá trị nhỏ nhất của biểu thức

A= (x+3)²+(x-5)²

2. tìm giá trị lớn nhất của biểu thức

A= x²+y² với x+3y=10

#Toán lớp 8

Nguyễn Lê Phước Thịnh

27 tháng 12 2021

Bài 1:

$A=x^2+6x+9+x^2-10x+25$

$=2x^2+4x+34$

$=2\left(x^2+2x+17\right)$

$=2\left(x+1\right)^2+32>=32\forall x$

Dấu '=' xảy ra khi x=-1

Đúng(1)

19.8A Trà My

27 tháng 12 2021

giải cho mình bài 2 lun đc ko

Đúng(0)

hoang

13 tháng 7 2016 - olm

Tìm giá trị lớn nhất của đa thức: D = -3X (X+3) -7

Tìm giá trị nhỏ nhất của đa thức: A= X^2 + 5X +8

B= x (x trừ 6)

#Toán lớp 8

^($_DUY_$)^

15 tháng 11 2023

Tìm giá trị nhỏ nhất của các phân thức sau
$B=\dfrac{x^2-2x+2016}{x^2}$

#Toán lớp 8

HT.Phong (9A5)

CTVHS

16 tháng 11 2023

Ta có:

$B=\dfrac{x^2-2x+2016}{x^2}\left(x\ne0\right)$

$B=\dfrac{x^2}{x^2}-\dfrac{2x}{x^2}+\dfrac{2016}{x^2}$

$B=1-\dfrac{2}{x}+\dfrac{2016}{x^2}$

$B=2016\left(\dfrac{1}{x^2}-\dfrac{1}{2016}\cdot\dfrac{2}{x}+\dfrac{1}{2016}\right)$

$B=2016\cdot\left(\dfrac{1}{x^2}-2\cdot\dfrac{1}{2016}\cdot\dfrac{1}{x}+\dfrac{1}{2016}\right)$

$B=2016\left(\dfrac{1}{x^2}-2\cdot\dfrac{1}{2016}\cdot\dfrac{1}{x}+\dfrac{1}{4064256}+\dfrac{2015}{4064256}\right)$

$B=2016\left[\dfrac{1}{x^2}-2\cdot\dfrac{1}{2016}\cdot\dfrac{1}{x}+\dfrac{1}{4064256}\right]+2016\cdot\dfrac{2015}{4064256}$

$B=2016\cdot\left(\dfrac{1}{x}-\dfrac{1}{2016}\right)^2+\dfrac{2015}{2016}$

Ta có: $2016\cdot\left(\dfrac{1}{x}-\dfrac{1}{2016}\right)^2\ge0\forall x$

$\Rightarrow2016\cdot\left(\dfrac{1}{x}-\dfrac{1}{2016}\right)^2+\dfrac{2015}{2016}\ge\dfrac{2015}{2016}\forall x$

Dấu "=" xảy ra khi:

$2016\cdot\left(\dfrac{1}{x}-\dfrac{1}{2016}\right)^2+\dfrac{2015}{2016}=\dfrac{2015}{2016}$

$\Leftrightarrow2016\cdot\left(\dfrac{1}{x}-\dfrac{1}{2016}\right)^2=0$

$\Leftrightarrow\dfrac{1}{x}-\dfrac{1}{2016}=0$

$\Leftrightarrow\dfrac{1}{x}=\dfrac{1}{2016}$

$\Leftrightarrow x=2016\left(tm\right)$

Vậy: $B_{min}=\dfrac{2015}{2016}\Leftrightarrow x=2016$

Đúng(2)

HT.Phong (9A5)

CTVHS

16 tháng 11 2023

Em nghĩ khi càng lớn thì B càn nhỏ ạ vì nếu thay x = 3 vào B thì giá trị của B gần bằng 224 còn nếu x = 10 thì B là 20,96 nên giá trị x = 1 chưa phải là GTNN của B ạ

Đúng(0)

Hùng Chu

20 tháng 6 2021

Cho biểu thức A=($\dfrac{x^2}{x^3-4x}+\dfrac{6}{6-3x}+\dfrac{1}{x+2}$):(x-2 + $\dfrac{10-x^2}{x+2}$)

a)Rút gọn A

b)Tính giá trị x của A với giá trị của x thỏa mãn |2x-1|=3

c) Tìm x để (3-4x).A<3

d) Tìm giá trị nhỏ nhất của biểu thức B=(8-$^{x^3}$).A+x

#Toán lớp 8

Lê Thị Hương Giang

30 tháng 10 2015 - olm

a/Tìm x để biểu thức sau có giá trị nhỏ nhất: (x^2)+x+1.

b/Tìm giá trị nhỏ nhất của biểu thức: A=y*(y+1)*(y+2)*(y+3).

c/Phân tích đa thức thành nhân tử: (x^3)+(y^3)+(z^3)-(3*x*y*z)

#Toán lớp 8

Nguyễn Ngọc Uyển Vy

31 tháng 10 2015

BÀI 2 a, x²+x+1=(x²+1/2*2*x+1/4)-1/4+1=(x+1/2)² +3/4

MÀ (x+1/2)²>=0 với mọi giá trị của x .Dấu"=" xảy ra khi x+1/2=0 =>x=-1/2

=>(x+1/2)²+3/4>=3/4 với mọi giá trị của x .Dấu "=" xảy ra khi x=-1/2

=>x²+x+1 có giá trị nhỏ nhất là 3/4 khi x=-1/2

b,A=y(y+1)(y+2)(y+3)

=>A =[y(y+3)] [(y+1)(y+2)]

=>A=(y²+3y) (y²+3y+2)

Đặt X=y²+3y+1

=>A=(X+1)(X-1)

=>A=X²-1

=>A=(y²+3y+1)²-1

MÀ (y²+3y+1)²>=0 với mọi giá trị của y

=>(y²+3y+1)²-1>=-1

Vậy GTNN của Alà -1

c,B=x³+y³+z³-3xyz

=>B=(x³+y³)+z³-3xyz

=>B=(x+y)³-3xy(x+y)+z³-3xyz

=>B=[(x+y)³+z³]-3xy(x+y+z)

=>B=(x+y+z)(x²+2xy+y²-xz-yz+z²)-3xy(x+y+z)

=>B=(x+y+z)(x²+2xy+y²-xz-yz+z²-3xy)

=>B=(x+y+z)(x²+y²+z²-xy-xz-yz)

Đúng(0)

Nguyễn Thiên Ngân

14 tháng 10 2018 - olm

Tìm giá trị nhỏ nhất của biểu thức: D=x^2+y^2-4(x+y)+16

#Toán lớp 8

Girl

14 tháng 10 2018

$D=x^2+y^2-4x-4y+16$

$D=\left(x^2-4x+4\right)+\left(y^2-4y+4\right)+8$

$D=\left(x-2\right)^2+\left(y-2\right)^2\ge8$

$"="\Leftrightarrow x=y=2$

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP