Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

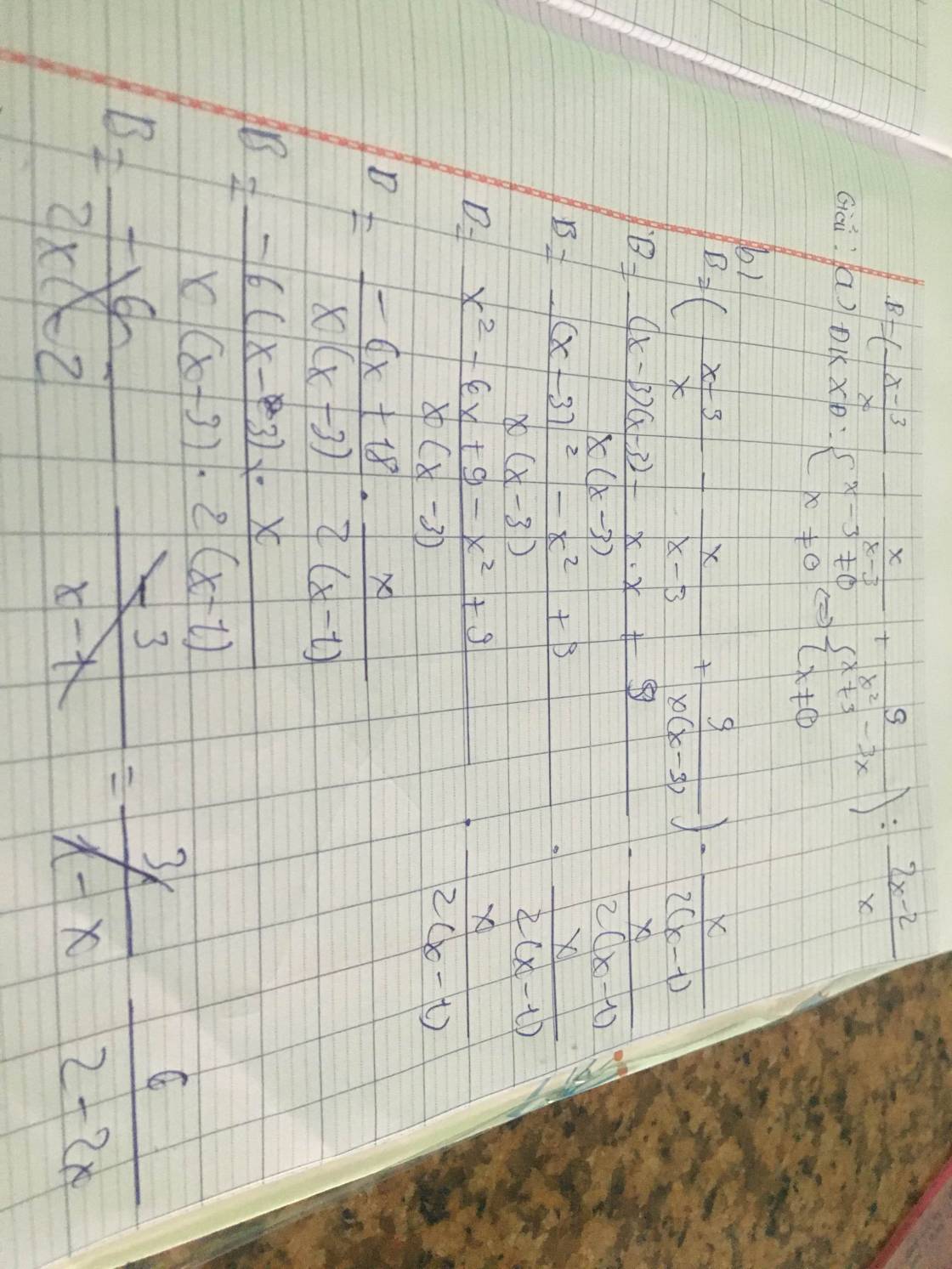
a: \(P=\left(\dfrac{-\left(x+3\right)}{x-3}+\dfrac{x-3}{x+3}+\dfrac{4x^2}{x^2-9}\right):\dfrac{2x+1-x-3}{x+3}\)
\(=\dfrac{-x^2-6x-9+x^2-6x+9+4x^2}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x-2}\)
\(=\dfrac{4x^2-12x}{x-3}\cdot\dfrac{1}{x-2}=\dfrac{4x}{x-2}\)
b: \(2x^2-5x+2=0\)
=>(x-2)(2x-1)=0
=>x=1/2
Thay x=1/2 vào P, ta được:
\(P=\left(4\cdot\dfrac{1}{2}\right):\left(\dfrac{1}{2}-2\right)=2:\dfrac{-3}{2}=\dfrac{-4}{3}\)

Bài 3:
a: =>3x^2-6x-x-3x^2=14
=>-7x=14
=>x=-2
b: \(\Leftrightarrow2x^2+10x-x-5-2x^2-9x-x-4.5=3.5\)
=>-x-9,5=3,5
=>-x=12
=>x=-12
c: =>\(3x-3x^2+9x=36\)
=>-3x^2+12x-36=0
=>x^2-6x+12=0(loại)
d: \(\Leftrightarrow3x^2-3x+x-1+4x-3x^2=5\)
=>2x=6
=>x=3

 c/
c/
Ta có : B=2=>6/2-2x
<=>6=4-4x
<=>6-4=-4x
<=>-4x=2
<=>x=2/-4=-1/2
d/ĐKXĐ:2-2x≠0
<=>2(1-x)≠0<=>-2(x-1)≠0
<=>x≠1
Để giá trị của biểu thức B nguyên thì 2-2x là Ư(6)
=>2-2x ∈ Ư(6)={±1;±2;±3;±6) Nếu 2-2x=1=> -2x=-1=>x=1/2( thoả mãng)
Rồi còn nhiêu bạn tự xét trường hợp y trang cách làm ở trênn nnhan :;)).À sẽ có mấy cái trường hợp nó giống ĐKXĐ thì bạn ghi trong ngoặc ko thoã mãn nhan.

\(\left(\frac{1}{x+1}-\frac{3}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{3}{x^2-x+1}\right).\frac{3\left(x^2-x+1\right)}{\left(x+1\right)\left(x+2\right)}-\frac{2\left(x-1\right)}{x+1}\)
\(\left(\frac{x^2-x+1}{x^3+1}-\frac{3}{x^3+1}+\frac{3\left(x+1\right)}{x^3+1}\right).\frac{3\left(x^2-x+1\right)}{\left(x+1\right)\left(x+2\right)}-\frac{2\left(x-1\right)}{x+1}\)
\(\left(\frac{x^2-x+1-3+3x+3}{x^3+1}\right).\frac{3\left(x^2-x+1\right)}{\left(x+1\right)\left(x+2\right)}-\frac{2\left(x-1\right)}{x+1}\)
tới đây bạn biến đổi tiếp, gõ = cái này lâu quá, gõ mathtype nhanh hơn

a)Đk:\(\left\{{}\begin{matrix}x^2-4\ne0\\2x^2-x^3\ne0\\x^2-3x\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)\left(x+2\right)\ne0\\x^2\left(2-x\right)\ne0\\x\left(x-3\right)\ne0\end{matrix}\right.\)\(\Leftrightarrow x\ne\left\{2;-2;0;3\right\}\)
b)\(P=\left[\dfrac{\left(2+x\right)^2}{\left(2+x\right)\left(2-x\right)}+\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{\left(2-x\right)^2}{\left(2+x\right)\left(2-x\right)}\right]:\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(=\dfrac{\left(2+x\right)^2-4x^2-\left(2-x\right)^2}{\left(2+x\right)\left(2-x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}\)
\(=\dfrac{4+4x+x^2-4x^2-4+4x-x^2}{\left(2+x\right)\left(2-x\right)}.\dfrac{x\left(2-x\right)}{x-3}\)
\(=\dfrac{x\left(8x-4x^2\right)}{\left(2+x\right)\left(x-3\right)}\) (sai đề chỗ nào ko em)
c)\(\left|x-5\right|=2\Leftrightarrow\left[{}\begin{matrix}x-5=2\\x-5=-2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=7\left(tm\right)\\x=3\left(ktm\right)\end{matrix}\right.\)
Thay x=7 vào bt P ta được: \(P=\dfrac{7\left(8.7-4.7^2\right)}{\left(2+7\right)\left(7-3\right)}=-\dfrac{245}{9}\)

Ta có:(12x^3-7x^2-14x+14): (4x-5)= (3x^2+2x-1)+9: (4x-5). Để (12x^3-7x^2-14x+14)chia hết cho (4x-5) thì 9 phải chia hết cho(4x-5).=>4x-5 thuộc vào ước của 9=+-1;+-3;+-9.xét từng giá trị để tìm x thỏa mãn khi x<0. Sau đó kết luận.

Lời giải:
$M=\frac{2x^2-3x+3}{x-2}=\frac{(2x^2-4x)+(x-2)+5}{x-2}$
$=\frac{2x(x-2)+(x-2)+5}{x-2}=2x+1+\frac{5}{x-2}$
Với $x$ nguyên, để $M$ nguyên thì $\frac{5}{x-2}$ nguyên
$\Rightarrow x-2$ là ước của $5$ (do $x$ nguyên)
$\Rightarrow x-2\in\left\{5;-5;1;-1\right\}$
$\Rightarrow x\in\left\{7; -3; 3; 1\right\}$

a, ĐKXĐ: \(x\ne1;x\ne-1\)
b, Với \(x\ne1;x\ne-1\)
\(B=\left[\dfrac{x+1}{2\left(x-1\right)}+\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\left[\dfrac{x^2+2x+1+6-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\dfrac{5}{x^2-1}\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =4\)
=> ĐPCM