Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ gt ta có x^2+y^^2=xy+1
=>P=(x^2+y^2)^2-2x^2y^2-x^2y^2
=(xy+1)2-2x2y2-x2y2
=x2y2+xy+1-3x2y2=-2x2y2+xy+1
=......
\(1=x^2+y^2-xy\ge2xy-xy=xy\Rightarrow xy\le1\)
\(1=x^2+y^2-xy\ge-2xy-xy=-3xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(\Rightarrow-\dfrac{1}{3}\le xy\le1\)
\(P=\left(x^2+y^2\right)^2-2\left(xy\right)^2-\left(xy\right)^2=\left(xy+1\right)^2-3\left(xy\right)^2=-2\left(xy\right)^2+2xy+1\)
Đặt \(xy=t\in\left[-\dfrac{1}{3};1\right]\)
\(P=f\left(t\right)=-2t^2+2t+1\)
\(f'\left(t\right)=-4t+2=0\Rightarrow t=\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow P_{max}=\dfrac{3}{2}\) ; \(P_{min}=\dfrac{1}{9}\)

Ta có y= 3-x≥ 1 nên x≤ 2 do đó : x
Khi đó P= x3+ 2( 3-x) 2+ 3x2+4x( 3-x) -5x= x3+x2-5x+18
Xét hàm số f(x) = x3+x2-5x+18 trên đoạn [0 ; 2] ta có:
f ' ( x ) = 3 x 2 + 2 x - 5 ⇒ f ' ( x ) = 0 x ∈ ( 0 ; 2 ) ⇔
F(0) =18; f(1) = 15; f(2) =20
Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P lần lượt bằng 20 và 15.
Chọn B.

Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
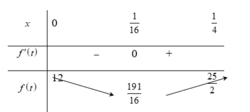
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
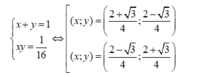
Chọn A.

Đáp án A
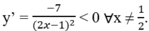
Suy ra hàm nghịch biến trên từng khoảng xác định, do đó hàm số nghịch biến trên đoạn [1; 4]. Vậy m = y(4) = 1; M = y(1) = 4 => d = M – m = 4 – 1 = 3

\(5^{x+3y}+5^{xy+1}+xy+1+x+3y=\frac{1}{5^{xy+1}}+\frac{1}{5^{x+3y}}\)
\(\Leftrightarrow5^{x+3y}-5^{-x-3y}+x+3y=5^{-xy-1}-5^{-\left(-xy-1\right)}+\left(-xy-1\right)\)
Xét hàm \(f\left(t\right)=5^t-\frac{1}{5^t}+t\Rightarrow f'\left(t\right)=5^t.ln5+\frac{ln5}{5^t}+1>0\)
\(\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow x+3y=-xy-1\)
\(\Rightarrow y\left(x+3\right)=-x-1\)
\(\Rightarrow y=\frac{-x-1}{x+3}\)
\(\Rightarrow T=f\left(x\right)=x-\frac{2x+2}{x+3}+1\)
\(f'\left(x\right)=\frac{\left(x+1\right)\left(x+5\right)}{\left(x+3\right)^2}>0;\forall x\ge0\)
\(\Rightarrow f\left(x\right)_{min}=f\left(0\right)=\frac{1}{3}\Rightarrow m=\frac{1}{3}\)

y ' = - 2 x - 1 2 < 0 trên đoạn [3; 5]. Vậy hàm số nghịch biến trên đoạn [3; 5].
Khi đó trên đoạn [-3,5]: hàm số đạt giá trị lớn nhất tại x = 3 và giá trị lớn nhất bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất = 1.5.

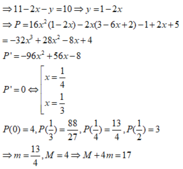


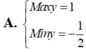
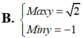
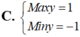
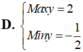
Do \(x+y=1\Rightarrow y=1-x\) nên \(P=5^{2x}+5^{1-x}=5^{2x}+\frac{5}{5^x}\)
Đặt \(t=5^x\) thì 1\(\le t\le\)5 ( do \(0\le x\le1\))
Xét hàm số \(f\left(t\right)=t^2+\frac{5}{t}\) với \(1\le t\le5\)
Ta có \(f'\left(t\right)=2t-\frac{5}{t^2}=\frac{2t^3-5}{t^2}\)
Do đó có bảng biến thiên
6 26
\(3\sqrt[3]{\frac{25}{4}}\)
Vậy min P=min f(t) = \(f\left(\sqrt[3]{\frac{5}{2}}\right)\)=\(3\sqrt[3]{\frac{25}{4}}\)
max P =max f(t) =f(5)=26