Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có bảng biến thiên như hình vẽ sau:
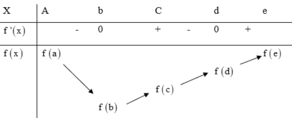
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.

Đáp án: A.
Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2
⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.
Cách khác: Vì a = -1 nên parabol y = -x2 + 4x - 5 đạt cực đại tại đỉnh (2; -1). Vì vậy GTLN của hàm số trên đoạn [0;3] là y(2) = -1

Đáp án: A.
Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2
⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.
Cách khác: Vì a = -1 nên parabol y = - x 2 + 4x - 5 đạt cực đạt tại đỉnh (2; -1). Vì vậy giá trị lớn nhất của hàm số trên đoạn [0;3] là y(2) = -1.

y ' = 3 x 2 + 6 x - m
Để hàm số đã cho đồng biến trên R khi và chỉ khi:
y ' = 3 x 2 + 6 x - m ≥ 0 ∀ x ∈ R
⇔ Δ = 9 + 3m ≤ 0 ⇔ m ≤ -3
Vậy giá trị lớn nhất của m để hàm số đã cho đồng biến trên R là m = -3.
Chọn A.

Lời giải:
a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)
Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.
$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học
$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)
Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$
$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky
$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$
Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$
c. ĐKXĐ: $-2\leq x\leq 2$
$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky
$\Leftrightarrow y^2\leq 8$
$\Leftrightarrow y\leq 2\sqrt{2}$
Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$
Mặt khác:
$x\geq -2$
$\sqrt{4-x^2}\geq 0$
$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$

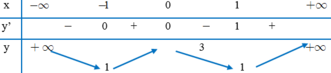

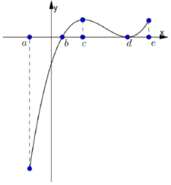
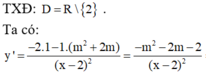

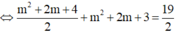
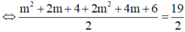
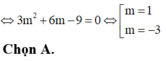
Đáp án A