
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số đo các góc A,B,C lần lượt là :a,b,c
Theo đề bài ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)và a+b+c=180*
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{180^o}{15}=12\)
\(\frac{a}{3}=12\Rightarrow a=12.3=36\)
\(\frac{b}{5}=12\Rightarrow12.5=60\)
\(\frac{c}{7}=12\Rightarrow12.7=84\)
Vậy số đo các góc A,B,C lần lượt là:36 ;60 ;84

a.
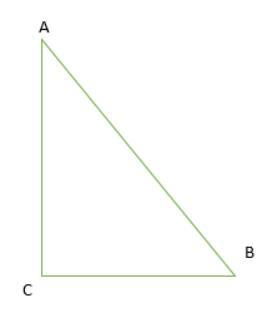
Góc CAB có số đo là 40 độ
Góc ABC có số đo là 50 độ
Góc ACB có số đo là 90 độ
b. Tổng ba góc trong tam giác là: 180 độ bằng với kết quả của các bạn khác.

1. Điền hạng tử thích hợp vào chố dấu * để mỗi đa thức sau trở thành bình phương của một tổng hoặc một hiệu.
a) 16x2 + * .24xy + x
b) * - 42xy + 49y2
c) 25x2 + * + 81
d) 64x2 - * +9
2. Viết mỗi bt sau về dạng tổng hoặc hiệu hai bình phương
a) x2 + 10x + 26 + y2 + 2y
b) z2 - 6z + 5 - t2 - 4t
c) x2 - 2xy + 2y2 + 2y + 1
d) ( x + y + 4 )( x + y - 4 )
e) ( x + y - 6 )

1. Điền hạng tử thích hợp vào chố dấu * để mỗi đa thức sau trở thành bình phương của một tổng hoặc một hiệu.
a) 16x2 + * .24xy + x
b) * - 42xy + 49y2
c) 25x2 + * + 81
d) 64x2 - * +9
2. Viết mỗi bt sau về dạng tổng hoặc hiệu hai bình phương
a) x2 + 10x + 26 + y2 + 2y
b) z2 - 6z + 5 - t2 - 4t
c) x2 - 2xy + 2y2 + 2y + 1
d) ( x + y + 4 )( x + y - 4 )
e) ( x + y - 6 )
gọi 3 canh của tam giác là a,b,c
mà độ dài các cạnh của tam giác tỉ lệ với 2,3,4
suy ra a/2=b/3=c/4= a+b+c/2+3+4= 20
nên a/2= 20 suy ra a=40
b/3=20 suy ra b=60
c/4=20 suy ra c=80
vậy chiều cao tương ứng của tam giác tỉ lệ với nhau theo tỉ số 40,60,80

Giải
a) Xét \(\Delta ABC\) ta có :
\(\widehat{B}=\widehat{A}+\widehat{C}=180^0\) ( Định lí tổng 3 góc của 1 tam giác )
\(\widehat{B}=90^0+32^0=180^0\)
\(\widehat{B}=122^0=180^0\)
\(\widehat{B}=180^0-122^0=58^0\)
b)
Theo bài ra ta có : \(\widehat{A}:\widehat{B}:\widehat{C}=2:7:1\)
\(\Rightarrow\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{7}=\dfrac{\widehat{C}}{1}\)
Lại có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( Định lí tổng 3 góc của 1 tam giác )
Áp dụng tính chất của dãy tỉ số bằng nhau nên ta có :
\(\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{7}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{2+7+1}=\dfrac{180^0}{10}=18^0\)
\(+)\)\(\dfrac{\widehat{A}}{2}=18^0\Rightarrow\widehat{A}=18^0\times2=36^0\)
\(+)\)\(\dfrac{\widehat{B}}{7}=18^0\Rightarrow\widehat{B}=18^0\times7=126^0\)
\(+)\)\(\dfrac{\widehat{C}}{1}=18^0\Rightarrow\widehat{C}=18^0\times1=18^0\)
c)
Xét \(\Delta ABC\) ta có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( Định lí trong 3 góc cùng 1 tam giác )
\(\widehat{A}+75^0+\widehat{C}=180^0\)
\(\widehat{A}+\widehat{C}=180^0-75^0\)
\(\widehat{A}+\widehat{C}=105^0\)
Theo bài ra ta có :
\(\widehat{A}:\widehat{C}=3:2\Rightarrow\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau nên ta có :
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{C}}{2}=\dfrac{\widehat{A}+\widehat{C}}{3+2}=\dfrac{105^0}{5}=21^0\)
\(+)\)\(\dfrac{\widehat{A}}{3}=21^0\Rightarrow\widehat{A}=21^0\times3=63^0\)
\(+)\)\(\dfrac{\widehat{C}}{2}=21^0\Rightarrow\widehat{C}=21^0\times2=42^0\)

a, góc xoy= 180 độ : 3= 60 độ
góc yoz = 60 độ x 2= 120 độ
b, do om là tia phân giác của góc yoz nên góc zom= góc yom = \(\frac{1}{2}\)góc yoz= 120độ :2= 60 độ
tức là góc yoz=góc yom= 60 độ
góc xoz= 180 độ
c, ot là góc nào, sao ko có trong đề.
thế thì oy là tia phân giác của góc nào và chứng minh

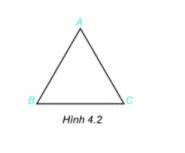
1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o
Ta có : tổng các góc = 180 o
Tổng số phần của các góc là :
2 + 3 + 4 = 9 phần
Số đo của góc thứ nhất là :
\(180:9\times2=40^o\)
Số đo của góc thứ 2 là :
\(180:9\times3=60\)
Số đo của góc thứ 3 là :
\(180:9\times4=80^o\)
Đáp số : .................