
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: A = |x + 1| + |x - 2009|
=> A = |x + 1| + |2009 - x| \(\ge\)|x + 1 + 2009 - x| = |2010| = 2010
Dấu "=" xảy ra <=> (x + 1)(2009 - x) \(\ge\)0
<=> \(-1\le x\le2009\)
Vậy MinA = 2010 khi \(-1\le x\le2009\)
b) Ta có: 2n - 1 = 2(n - 4) + 7
Do 2(n - 4) \(⋮\)n - 4 => 7 \(⋮\)n - 4
=> n - 4 \(\in\)Ư(7) = {1; -1; 7; -7}
Lập bảng:
| n - 4 | 1 | -1 | 7 | -7 |
| n | 5 | 3 | 11 | -3 |
Vậy ....
a) Ta có A = |x + 1| + |x - 2009|
= |x + 1| + |2009 - x| \(\ge\left|x+1+2009-x\right|=2010\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-1\ge0\\2009-x\ge0\end{cases}}\Rightarrow\hept{\begin{cases}x\ge1\\x\le2009\end{cases}\Rightarrow1\le x\le2009}\)
b) Để 2n - 1 \(⋮\)n - 4
=> 2n - 8 + 7 \(⋮\)n - 4
=> 2(n - 4) + 7 \(⋮\)n - 4
Vì 2(n - 4) \(⋮\)n - 4
=> 7 \(⋮\)n - 4
=> \(n-4\inƯ\left(7\right)\Rightarrow n-4\in\left\{\pm1;\pm7\right\}\)
Lập bảng xét các trường hợp :
| n - 4 | 1 | -1 | 7 | -7 |
| n | 5 | 3 | 11 | -3 |
Vậy \(n\in\left\{-3;3;5;11\right\}\)

\(A=\frac{3x+2}{x-3}=\frac{3\left(x-3\right)+11}{x-3}=\frac{3\left(x-3\right)}{x-3}+\frac{11}{x-3}=3+\frac{11}{x-3}\left(ĐK:x\ne3\right)\)
Để A nguyên thì \(11⋮x-3\)hay \(x-3\inƯ\left(11\right)\)
| Ư(11) | x - 3 | x |
| 1 | 1 | 4 |
| -1 | -1 | 2 |
| 11 | 11 | 14 |
| -11 | -11 | -8 |
Vậy để A nguyên \(x\in\left\{4;2;14;-8\right\}\)

Theo đề bài, ta có: \(3x-4⋮x-1\)
\(\Rightarrow3\left(x-1\right)-1⋮x-1\)
\(\Rightarrow-1⋮x-1\)
Vì \(x\in Z\Rightarrow x-1\inƯ\left(-1\right)=\left\{\mp1\right\}\)
Ta có các trường hợp sau:
\(\orbr{\begin{cases}x-1=1\\x-1=-1\end{cases}}\Rightarrow\orbr{\begin{cases}x=2\\x=0\end{cases}}\)
Vậy \(x\in\left\{2;0\right\}\)

x^3+3x-5 chia hết cho x^2+2
=>x^3+2x+x-5 chia hết cho x^2+2
=>x-5 chia hết cho x^2+2
=>x^2-25 chia hết cho x^2+2
=>x^2+2-27 chia hết cho x^2+2
=>x^2+2 thuộc Ư(-27)
=>x^2+2 thuộc {3;9;27}
=>\(x\in\left\{1;-1;5;-5\right\}\)

Bài 1:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{a+b+c}{b+c+d}\)
hay \(\frac{a}{b}=\frac{a+b+c}{b+c+d}\)
\(\frac{b}{c}=\frac{a+b+c}{b+c+d}\)
\(\frac{c}{d}=\frac{a+b+c}{b+c+d}\)
Nhân vế theo vế của 3 đẳng thức trên ta có:
\(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)
mà \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=\frac{a}{d}\)
\(\Rightarrow\left(\frac{a+b+c}{b+c+d}\right)^3=\frac{a}{d}\left(đpcm\right)\)
Bài 2: Không làm được, thông cảm. Gợi ý: Áp dụng chia tỉ lệ

a) Ta có : x - 4 chia hết cho x + 1
=> x + 1 - 5 chia hết cho x + 1
=> 5 chia hết cho x + 1
=> x + 1 thuộc Ư(5) = {-5;-1;1;5}
=> x = {-6;-2;0;4}
b) 3x - 1 chia hết cho x - 4
=> 3x - 12 + 11 chia hết cho x - 4
=> 3(x - 4) + 11 chia hết cho x - 4
=> 11 chia hết cho x - 4
=> x - 4 thuộc Ư(11) = {-11;-1;1;11}
=> x = {-7;3;5;15}
a,x-4 chia hết cho x+1
\(\Rightarrow\)x-(1+3) chia hết cho x+1
Mà x+1 chia hết cho x+1 nên 3 chia hết cho x+1
\(\Rightarrow\)x thuộc Ư(3)={1;3}
\(\Rightarrow\)x thuộc {0;2}


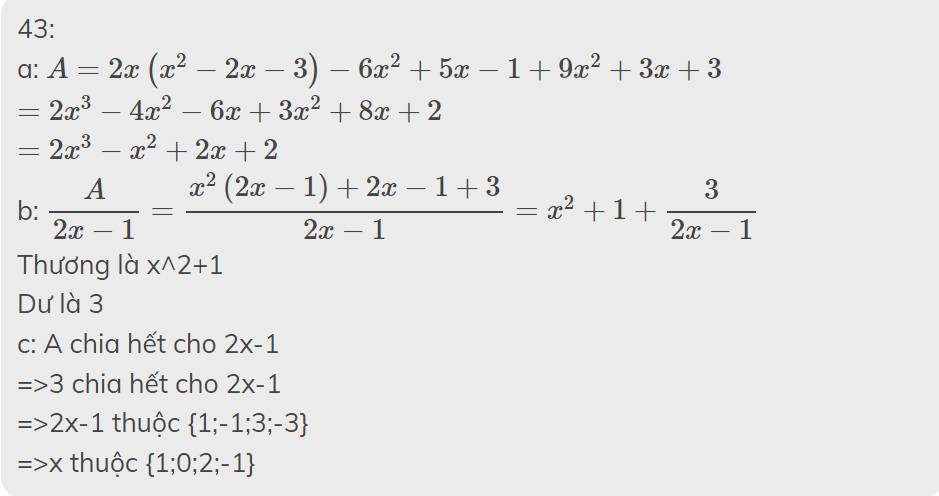
3x+2\(⋮\)x-1
<=> 3x - 3 + 5 \(⋮\)x - 1
Vì 3x - 3 \(⋮\)x - 1 mà 3x - 3 + 5 \(⋮\)x - 1 nên:
=> 5 \(⋮\)x - 1
x - 1 \(\in\){ -5;-1;1;5}
=> x \(\in\){ -4;0;2;6}
Vậy x = { -4;0;2;6}