Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c)chia hết cho 12 thì phải chia hết cho 4 và 3
=>7a chia hết cho 4 mà achia hết cho 3 nên a=2
d)2a5b chia hết cho 18 thì phải chia hết cho 2 và 9
=>các cặp số(a,b) là:
(2,0),(0,2),(7,4),(5,6),(3,8)

a. 15ab chia hét cho 2 & 5 => b=0
15a0 chia hết cho 3 => 1+5+0+a chia hết cho 3
hay 6+a chia hết cho 3
=> a \(\in\left\{0;3;6;9\right\}\)
b. ab+ba chia hết cho 33
=> ab+ba chia hết cho 11 & 3 (11.3=33)
=> 10a+b+10b+a chia hết cho 11 và 3
=> 11a+11b chia hết cho 11 và 3
=> 11(a+b) chia hết cho 3 (đã chia hết cho 11)
=> a+b chia hết cho 3
=> a+b là các số có tổng chia hết cho 3 (vd: a=1,b=2 có tổng là 3; a=2,b=4 có tổng là 6 chia hết cho 3;...)

Gỉai:
1.(ab + ba ) chia hết cho 9
=>9 : ab +ba
=>ab = một số ba=một số
=>Mà ba = 1 số
=>Vậy ba và ab vẫn =9
Hai số bằng nhau
Tương tự nhé
P.s:Not chắc

a, 23850
b,11850 hoặc 14850 hoặc 17850
c,14400 ; 14430 ;14460 ; 14490 ; 14415 ; 14445 ; 14475
d,5274
23x5y chia hết cho 2,5,9
Do 23x5y chia hết cho 2 và 5
\(\Rightarrow y=0\)
Thay y = 0 ta có:
23x50 chia hết cho 9
=> 2+3+x+5+0 chia hết cho 9
=> 10+x chia hết cho 9
=> x=8
Vậy số càn ìm là 23850
b) 1x85y chia hết cho 2,3,5
1x85y chia hết cho 2,5
=> y=0
Thay y=0 ta có:
1x850 chia hết cho 3
=> 1+x+8+5+0 chia hết cho 3
=> 13+x chia hết cho 3
\(\Rightarrow x\in\left\{2;5;8\right\}\)
Vậy các số cần tìm là 12850,15850,18850
c) 144xy chia hết cho 3,5
Vì 144xy chia hết cho 5
\(\Rightarrow y\in\left\{0;5\right\}\)
- Nếu y = 0 ta có: 144x0 chia hết cho 3 => 9+x chia hết cho 3 \(\Rightarrow x\in\left\{0;3;6;9\right\}\)
- Nếu y = 5 ta có: 144x5 chia hết cho 3 => 14+x chia hết cho 3 \(\Rightarrow x\in\left\{1;4;7\right\}\)
d) 52xy chia hết cho 9,2 và chia 5 dư 4
Do 52xy chia hết 2 và chia 5 dư 4
=> y = 4
Thay y = 4 ta có:
52x4 chia hết cho 9
=> 11 + x chia hết cho 9
=> x = 7


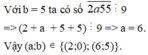
a)1530;1560
b)30+03;60+06;........
li ke nha
Nhưng mà làm cách nào chứ bạn