Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


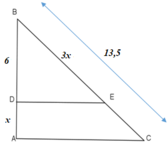
Ta có: ED ⊥ AB, AC ⊥ AB => DE // AC (từ vuông góc đến song song), áp dụng định lý Talet, ta có: B D D A = B E E C
⇔ x 2 + 6 x – 27 = 0
Vậy x = 3
Đáp án: A



Áp dụng bất đẳng thức Cô - si ta có:
\(S\) \(=\) \(ab+\dfrac{1}{ab}\ge2\sqrt{ab.\dfrac{1}{ab}}\)
\(S\) \(=\) \(ab+\dfrac{1}{ab}\ge2\sqrt{1}=2\)
Dấu " = " xảy ra khi \(\left\{{}\begin{matrix}ab=\dfrac{1}{ab}\\a+b=1\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}\left(ab\right)^2=1\\a+b=1\end{matrix}\right.\)
⇔ \(a=b=0,5\)
GTNN của \(S=ab+\dfrac{1}{ab}=2\) khi \(a=b=0,5\)
S=\(ab+\dfrac{1}{ab}\)
Ta có :
Áp dụng BĐT Cauchy(cô-sy),ta có
1\(\ge a+b\ge2\sqrt{ab}\)\(\Leftrightarrow\sqrt{ab}\le\dfrac{1}{2}\)\(\Rightarrow ab\le\dfrac{1}{4}\)
Đặt x=ab(x\(\le\dfrac{1}{4}\))
\(\Rightarrow x+\dfrac{1}{x}=x+\dfrac{1}{16x}+\dfrac{15}{16x}\)
Áp dụng BĐT Cauchy (Cô -si):
\(S\ge2\sqrt{\dfrac{1}{16}}+\dfrac{15}{16x}=\dfrac{1}{2}+\dfrac{15}{16X}\ge\dfrac{1}{2}+\dfrac{16}{16.\dfrac{1}{4}}=\dfrac{17}{4}\)
Vậy Min S=\(\dfrac{17}{4}\) \(\Leftrightarrow\left\{{}\begin{matrix}a+b=1\\ab=\dfrac{1}{16ab}\\ab=\dfrac{1}{4}\\\end{matrix}\right.\) \(\Leftrightarrow a=b=\dfrac{1}{2}\)


Ta có: a/b = ab => ab/b^2 = ab => b^2 = 1 => b = 1 hoặc -1
Với b = 1, a + b = a.b => a + 1 = a (vô lí)
Với b = - 1, a + b = ab => a -1 = -a => 2a = 1 => a = 1/2 (thỏa Đk)
Vậy cặp số hữu tỉ cần tìm là 1/2 và -1

a: Sửa đề: \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(hai góc đồng vị, MN//BC)
\(\widehat{A}\) chung
Do đó: ΔAMN đồng dạng với ΔABC
=>\(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
b: \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
=>\(\dfrac{MN}{8}=\dfrac{2}{5}\)
=>\(MN=2\cdot\dfrac{8}{5}=\dfrac{16}{5}\)

\(\left\{{}\begin{matrix}a^2+b^2=32\\a+b+2ab=40\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2+2ab+a+b=72\\a+b+2ab=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a+b\right)^2+\left(a+b\right)-72=0\\a+b+2ab=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a+b=8\\a+b=-9\end{matrix}\right.\\a+b+2ab=40\end{matrix}\right.\)
TH1: \(a+b=8\Rightarrow ab=16\)
\(\Rightarrow a\left(8-a\right)=16\Leftrightarrow a^2-8a+16=0\)
\(\Leftrightarrow\left(a-4\right)^2=0\Rightarrow a=4\Rightarrow b=4\)
TH2: \(a+b=-9\Rightarrow ab=\dfrac{49}{2}\)
\(\Rightarrow a\left(-9-a\right)=\dfrac{49}{2}\) \(\Leftrightarrow2a^2+18a+49=0\)
\(\Leftrightarrow2\left(a+\dfrac{9}{2}\right)^2+\dfrac{17}{2}=0\) (ko tồn tại a thỏa mãn)
Vậy \(\left\{{}\begin{matrix}a=4\\b=4\end{matrix}\right.\)
Cách 2:
Với mọi số thực a; b ta luôn có:
\(\left(a-4\right)^2+8\left(a-b\right)^2+\left(b-4\right)^2\ge0\)
\(\Leftrightarrow a^2-8a+16+8\left(a^2-2ab+b^2\right)+b^2-8a+16\ge0\)
\(\Leftrightarrow9\left(a^2+b^2\right)\ge8\left(a+b+2ab\right)-32\)
\(\Leftrightarrow9\left(a^2+b^2\right)\ge288\)
\(\Leftrightarrow a^2+b^2\ge32\)
Đẳng thức xảy ra khi và chỉ khi \(a=b=4\)

ta có: a+b=35 suy ra a=35-b
a*b=300 suy ra a=300:b
35-b=300:b
suy ra b*(35-b)=300
35b-b^2=300
suy ra 35b-b-300=0
-b^2+35b-300=0
-(b^2-35b+300)=0
-(b^2-2b17,5+17,5^2+300-17,5^2)=0
-(b-17,5)^2-6,25=0
6,25-(b-17,5)^2=0
2,5^2-(b-17,5)^2=0
(2,5-b+17,5)(2,5+b-17,5)=0
(20-b)(15-b)=0
20-b=0 b=20
hoặc 15-b=0 b=15
nếu b=20 thì a=15
nếu b=15 thì a=20
vậy a=15 ; b=20 hay ngược lại