
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Đáp án D.
Hai đường thẳng d và d ' cắt nhau khi và chỉ khi hệ phương trình
1 + a 2 t = 3 − t ' t = 2 + t ' − 1 + 2 t = 3 − t ' có đúng một nghiệm ⇔ t = 2 t ' = 0 a = ± 1 .
Vậy ta chọn D.

Đáp án A
Ta nhận thấy (D) song song với các đường ( d 2 ); ( d 3 ); ( d 4 ).

Chọn C.
Phương pháp: Sử dụng phương trình hoành độ giao điểm và định lý Viet.
Cách giải: Phương trình hoành độ giao điểm là

Vì a,c là nghiệm của (*) nên theo định lý Viet ta có:
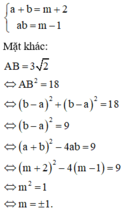

Đáp án D
Phương trình hoành độ giao điểm x + m = 2 x x + 1 x ≠ − 1 ⇔ x 2 + m + 1 x + m ∀ x ≠ 1 = 2 x
⇔ x 2 + m − 1 x + m = 0 x ≠ − 1 Để d cắt đồ thị hàm số y = 2 x x + 1 tại 2 điểm phân biệt ⇔ g x = x 2 + m − 1 x + m = 0 có 2 nghiệm phân biệt khác .
Khi đó g − 1 = 2 ≠ 0 Δ = m − 1 2 − 4 m > 0 ⇒ m > 3 + 2 2 m < 3 − 2 2



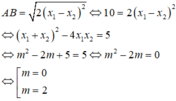

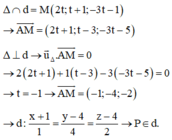
Xét hệ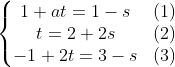
Hai đường thẳng d và d' cắt nhau khi và chỉ khi hệ có nghiệm duy nhất.
Nhân hai về của phương trình (3) với 2 rồi cộng vế với vế vào phương trình (2), ta có t = 2;
s = 0. Thay vào phương trình (1) ta có 1 + 2a = 1 => a =0.
Vậy a = 0 thì d và d' cắt nhau.