
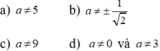
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

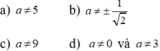

C nhé
Vì;Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b < 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a và b là hai số đã cho, a# 0, được gọi là bất phương trình bậc nhất một ẩn.
NHỚ K NHA
Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b < 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a và b là hai số đã cho, a# 0, được gọi là bất phương trình bậc nhất một ẩn.
chọn C

1. Trong các phương trình sau, phương trình bậc nhất 1 ẩn là
A. 2/x - 7=0; B. |7x+5)-1=0; C. 8x-9=0
2. điều kiện xác định của phương trình
\(\frac{4}{2x-3}=\frac{7}{3x-5}\)là
A. x khác 3/2. B. x khác5/3; C. x khác 3/2 hoặc 5/3; D. x khác 3/2 và 5/3
1.Pt bậc nhất 1 ẩn:\(8x-9=0\)
2.ĐKXĐ:\(x\ne\frac{3}{2};x\ne\frac{5}{3}\)

ĐKXĐ:\(x\ne\pm2;x\ne-3;x\ne0\)
\(P=1+\frac{x-3}{x^2+5x+6}\left(\frac{8x^2}{4x^3-8x^2}-\frac{3x}{3x^2-12}-\frac{1}{x+2}\right)\)
\(=1+\frac{x-3}{\left(x+2\right)\left(x+3\right)}\left[\frac{8x^2}{4x^2\left(x-2\right)}-\frac{3x}{3\left(x^2-4\right)}-\frac{1}{x+2}\right]\)
\(=1+\frac{x-3}{\left(x+2\right)\left(x+3\right)}\left(\frac{2}{x-2}-\frac{x}{x^2-4}-\frac{1}{x+2}\right)\)
\(=1+\frac{x-3}{\left(x+2\right)\left(x+3\right)}\left[\frac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\frac{x}{\left(x-2\right)\left(x+2\right)}-\frac{x-2}{\left(x-2\right)\left(x+2\right)}\right]\)
\(=1+\frac{x-3}{\left(x+2\right)\left(x+3\right)}\cdot\frac{2x+4-x-x+4}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\frac{8\left(x-3\right)}{\left(x+2\right)^2\left(x+3\right)\left(x-2\right)}\)
Đề sai à ??

bất phương trình bậc nhất 1 ẩn là a, b, d
a) -1/2x+5>_0
<=> 2x+5>_0
<=> 2x>_-5
<=> 2x.1/2>_-5.1/2
<=>x>_-5/2
Vậy tập nghiệm của bpt S={x/x>_-5/2}
b) 2x+3/4<0
<=> 2x+3<0
<=> 2x<-3
<=> 2x.1/2<-3.1/2
<=> x<-3/2
Vậy tập nghiệm của bpt S={x/x<-3/2}
d)5-2x<0
<=> -2x<-5
<=>-2x.-1/2>-5.-1/2
<=> x>5/2
Vậy tập nghiệm của bpt S={x/x>5/2}

a) \(\left(x+\frac{1}{9}\right)\left(2x-5\right)< 0\)
TH1 : \(\hept{\begin{cases}x+\frac{1}{9}>0\\2x-5< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>\frac{-1}{9}\\x< \frac{5}{2}\end{cases}}\)
\(\Leftrightarrow\frac{-1}{9}< x< \frac{5}{2}\)( thỏa )
TH2 : \(\hept{\begin{cases}x+\frac{1}{9}< 0\\2x-5>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x< -\frac{1}{9}\\x>\frac{5}{2}\end{cases}}\)
\(\Leftrightarrow\frac{5}{2}< x< -\frac{1}{9}\)( loại )
Vậy....
b) \(x^2-6x+9< 0\)
\(\Leftrightarrow\left(x-3\right)^2< 0\)( vô lý )
Vậy bpt vô nghiệm