Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

search mạn bn à. Mà bài này dễ CM mà công thức trong sách giáo khoa lớp 7 hả.......


\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\\ \Leftrightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)

Áp dụng t.c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\\ \Leftrightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)

\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\Rightarrow\frac{q^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}=\frac{a^2-b^2+2c^2}{4-9+32}=\frac{108}{27}=4\)
=> \(\frac{a^2}{4}=4\Rightarrow a^2=4.4=16\Rightarrow a=+-4\)
=>\(\frac{b^2}{9}=4\Rightarrow b^2=4.9=36\Rightarrow b=+-6\)
=>\(\frac{2c^2}{32}=4\Rightarrow c^2=4.32:2=64\Rightarrow c=+-8\)
Câu 2 :
Ta có : \(\frac{a}{b}=\frac{c}{d}\) \(\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\)
\(\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)

Cho \(\frac{a}{b}=\frac{c}{d}\) chứng minh rằng \(\frac{a}{a-b}=\frac{c}{c-d}\)
Có \(\frac{a}{a-b}=\frac{c}{c-d}\Leftrightarrow\frac{a-b}{a}=\frac{c-d}{c}\Leftrightarrow\frac{a}{a}-\frac{b}{a}=\frac{c}{c}-\frac{d}{c}\Leftrightarrow1-\frac{b}{a}=1-\frac{d}{c}\)
\(\Rightarrow\frac{b}{a}=\frac{d}{c}hay\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\)
Đề bài cho \(\frac{a}{b}=\frac{c}{d}\) \(\Rightarrow b=c.\) Không thể \(ad=bc\Rightarrow\) Đề sai
Ta có: \(\frac{a}{b}=\frac{c}{d}=k\left(k\ne0\right)\)
\(\Rightarrow a=kb,c=kd\)
Xét: \(\frac{a}{a-b}=\frac{bk}{bk-b}=\frac{bk}{b\left(k-1\right)}=\frac{k}{k-1}\left(1\right)\)
\(\frac{c}{c-d}=\frac{kd}{kd-d}=\frac{kd}{d\left(k-1\right)}=\frac{k}{k-1}\left(2\right)\)
Từ (1) và (2) => \(\frac{a}{a-b}=\frac{c}{c-d}\)
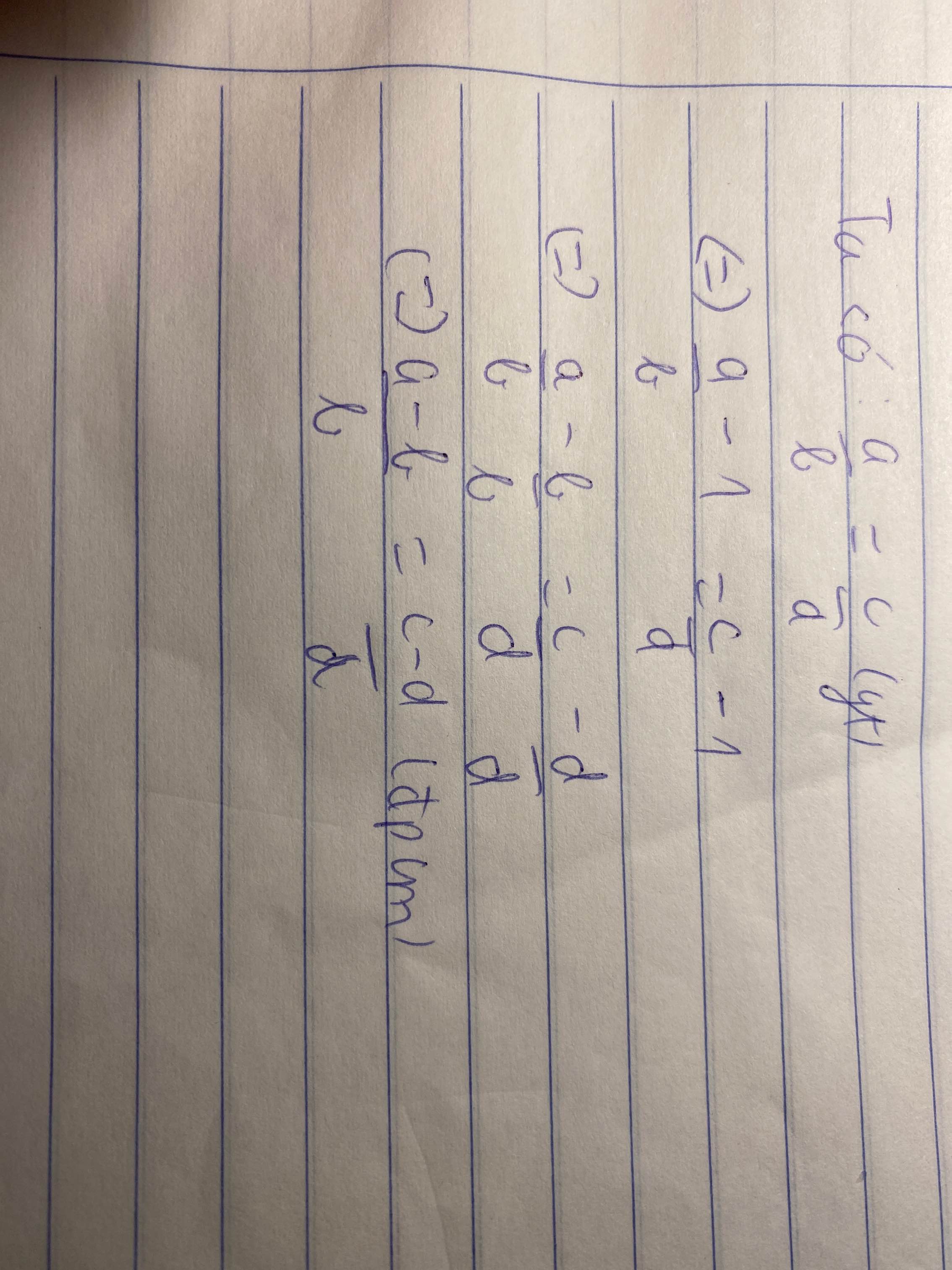
Dễ thể mà không ai trả lời
1)\(A=\dfrac{a}{b+c}=\dfrac{c}{a+b}=\dfrac{b}{c+a}\Leftrightarrow a\left(a+b\right)=c\left(c+a\right)=b\left(b+c\right)\Leftrightarrow a=b=c\)Do a = b = c nên ta có thể thế b + c =2a , a+b = 2c, c + a = 2b
Ta có: \(A=\dfrac{a}{2a}=\dfrac{b}{2b}=\dfrac{c}{2c}=\dfrac{1}{2}\) . Do đó \(A=\dfrac{1}{2}\)
2) Ta có: \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\) . Cần chứng minh: \(\dfrac{\left(a+b+c\right)^3}{\left(b+c+d\right)^3}=\dfrac{a}{d}\)
Từ giả thiết suy ra a = b = c =d
Theo giả thiết,áp dụng t/c dãy tì số bằng nhau.Ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}=\dfrac{a}{d}=1\)
Do đó \(\dfrac{\left(a+b+c\right)^3}{\left(b+c+d\right)^3}=1^3=1=\dfrac{a}{d}^{\left(đpcm\right)}\)
Dấu "=" xảy ra khi và chỉ khi a = b =c = d