CL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
NT
1
12 tháng 12 2015
tận cùng là 5 mũ 1 số lớn hơn 0 lúc nào chả có tận cùng là 5:v
KH
1
LT
1
4 tháng 10 2016
72367033806371673149109894141163778628811792657571658906010558390395870363798401744095280686155507736404921657070284961721828960592977909542637098897697223102622628566787654091327825453991595140205701412961364188732408936197890553699715836951569999800431957769217006743321026257517932764164662319487914962533302741368207211189494615326552790667720411285474162636765168907211924134973374304496019635376665858559941735703924836467756917247995469583487467791524582153744522107597865277798136080074161485280424274076931083994487111719562249702540362855712911132265966235754355353516703339043001506118520760359577737869472018617942120590873170710805078696371738906375721785723
4 chữ số tận cùng là 5723
12 tháng 9 2020
Ta có thể chứng minh bằng cách sau:
(10a+5)^2=(10a)^2+10.5.2.a+5^2
=100a^2+100.a+25
=100a*(a+1)+25
CM
3 tháng 2 2019
Ta có:
(10a + 5)2 = (10a)2 + 2.10a.5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25
Đặt A = a.(a + 1). Khi đó ta có:
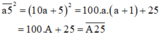
Do vậy, để tính bình phương của một số tự nhiên có dạng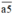 
, ta chỉ cần tính tích a.(a + 1) rồi viết 25 vào đằng sau kết quả vừa tìm được.
Áp dụng:
252 = 625 (Vì 2.3 = 6)
352 = 1225 (Vì 3.4 = 12)
652 = 4225 (Vì 6.7 = 42)
752 = 5625 (Vì 7.8 = 56)
21 tháng 6 2019
\(5^6\equiv1\left(mod8\right)\)
\(353\equiv5\left(mod6\right)\Rightarrow353^{81}\equiv5^{81}\equiv5\left(mod6\right)\)
Đặt: \(358^{81}=6t+5\)
=> \(5^{353^{81}}\equiv5^{6t+5}\equiv5^5\equiv5\left(mod8\right)\)
=>\(5^{353^{81}}-5-15.8\equiv0\left(mod8\right)\)
\(\Rightarrow5^{353^{81}}-125\equiv0\left(mod8\right)\)
mà : \(5^{353^{81}}\equiv0\left(mod125\right)\Rightarrow5^{353^{81}}-125\equiv0\left(mod125\right)\)
\(\Rightarrow5^{353^{81}}-125\equiv0\left(mod1000\right)\)
link kết quả 22015 nè: http://goo.gl/b951WQ