Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm là ab
Theo đề bài ta có:
2ab2=153.ab
ab.10+2002=153.ab
ab.143=2002
ab=2002:143
ab=14
Vậy số cần tìm là 14.
Chúc học tốt^^

Gọi x là số tự nhiên có hai chữ số 9<x<100 và x ∈ N
Nếu viết thêm một chữ số 2 vào bên trái và chữ số 2 vào bên phải số x ta được số tự nhiên có 4 chữ số là: 2×2 (x có 2 chữ số0
Ta có 2×2 =153x
Suy ra phương trình 2000 + 10x + 2 = 153x ⇔ 2002 = 143x ⇔ x =14
x= 14 thỏa mãn điều kiện bài toán nên số cần tìm là 14

Gọi số có hai chữ số cần tìm là 
Khi viết thêm một chữ số 2 vào bên trái và một chữ số 2 vào bên phải thì ta được số mới là
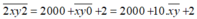
Theo đề bài, số mới gấp 153 lần số ban đầu nên ta có phương trình :
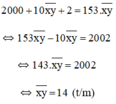
Vậy số cần tìm là 14.
* Lưu ý : Ở bài toán này ta coi cả số 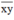 là một ẩn.
là một ẩn.
Các bạn có thể đặt ẩn đơn giản là x hoặc A … nhưng khi phân tích số  thì các bạn cần lưu ý nó là số có 4 chữ số nên
thì các bạn cần lưu ý nó là số có 4 chữ số nên 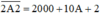 , nếu bạn phân tích thành
, nếu bạn phân tích thành 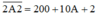 là sai.
là sai.

Đáp án B
Gọi số có hai chữ số cần tìm là 
Khi viết thêm một chữ số 2 vào bên trái và một chữ số 2 vào bên phải thì ta được số mới là 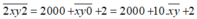
Theo đề bài, số mới gấp 153 lần số ban đầu nên ta có phương trình :
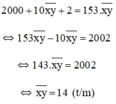
Vậy số cần tìm là 14.
* Lưu ý : Ở bài toán này ta coi cả số 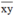 là một ẩn.
là một ẩn.
Các bạn có thể đặt ẩn đơn giản là x hoặc A … nhưng khi phân tích số  thì các bạn cần lưu ý nó là số có 4 chữ số nên
thì các bạn cần lưu ý nó là số có 4 chữ số nên 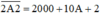 , nếu bạn phân tích thành
, nếu bạn phân tích thành 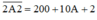 là sai.
là sai.

Gọi số đó là ab
sau khi thêm một chữ số 2 vào bên phải và 2 vào bên trái ta được số mới:
2ab2
Vì số mới gấp hai 153 số cũ nên ta có:
2ab2:ab=153
<=>2ab2=153.ab
<=>2000+100a+10b+2=153(10a+b)
<=>2002+100a+10b=1530a+153b
<=>2002=1530a-100a+153b-10b
<=>2002=1430a+143b
<=>2002=143(10a+b)
<=>10a+b=2002:143
<=>10a+b=14
=>ab=14
Gọi số đó là ab
sau khi thêm một chữ số 2 vào bên phải và 2 vào bên trái ta được số mới: 2ab2
Vì số mới gấp hai 153 số cũ nên ta có:
2ab2:ab=153
<=>2ab2=153.ab
<=>2000+100a+10b+2=153(10a+b)
<=>2002+100a+10b=1530a+153b
<=>2002=1530a-100a+153b-10b
<=>2002=1430a+143b <=>2002=143(10a+b)
<=>10a+b=2002:143
<=>10a+b=14
=>ab=14

Gọi số tự nhiên có hai chữ số ban đầu là x. (10 ≤ x ≤ 99; nguyên)
Vậy số tự nhiên cần tìm: 14
Gọi số tự nhiên có hai chữ số cần tìm là \(\overline{ab}\) ( \(\overline{ab}\)\(\in N\)*, 10\(\le\overline{ab}\le99\))
=> Số mới là \(\overline{2ab2}\)
Theo đề ta có:
\(\dfrac{\overline{2ab2}}{\overline{ab}}=153\)
<=> 153.\(\overline{ab}\)=\(\overline{2ab2}\)
<=>153.\(\overline{ab}\)=2000+\(\overline{ab}\).10+2
<=> 143\(\overline{ab}\)=2002
<=> \(\overline{ab}\)=14 (thỏa mãn điều kiện)
Vậy số tự nhiên có hai chữ số cần tìm là 14

gọi số đó là ab
sau khi thêm một chữ số 2 vào bên phải và 2 vào bên trái ta được số mới:
2ab2
vì số mới gắp hai 153 số cũ nên ta có:
2ab2:ab=153
<=>2ab2=153.ab
<=>2000+100a+10b+2=153(10a+b)
<=>2002+100a+10b=1530a+153b
<=>2002=1530a-100a+153b-10b
<=>2002=1430a+143b
<=>2002=143(10a+b)
<=>10a+b=2002:143
<=>10a+b=14
=>ab=14

Gọi số có 2 chữ số cần tìm là \(\overline{ab}\left(a\ne0,a;b\in N\right)\)
Khi viết thêm một chữ số 2 vào bên trái và 1 chữ số 2 vào bên phải thì được số mới \(\overline{2ab2}\)
Mà số mới hơn số cũ 135 lần nên ta có phương trình :
\(\overline{2ab2}\div\overline{ab}=135\)
\(\Leftrightarrow135\times\overline{ab}=\overline{2ab2}\)
\(\Leftrightarrow135\times\left(10a+b\right)=2000+100a+10b+2\)
\(\Leftrightarrow1350a+135b=2002+100a+10b\)
\(\Leftrightarrow1250a+125b=2002\)
\(\Leftrightarrow125\times\left(10a+b\right)=2002\)
\(\Leftrightarrow\overline{ab}=\frac{2002}{125}\)
\(\Rightarrow\) Sai đề.
