
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2xdx\\v=\dfrac{1}{2}sin2x\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{2}x^2sin2x|^{\pi}_0-\int\limits^{\pi}_0x.sin2xdx\)

Bạn nên viết đề bằng công thức toán để mọi người hiểu đề hơn

Đặt \(I=\dfrac{1}{2}\int\limits^{\dfrac{\pi}{2}}_0f\left(2sinx+1\right)d\left(2sinx+1\right)\)
Đặt \(2sinx+1=t\Rightarrow I=\dfrac{1}{2}\int\limits^3_1f\left(t\right)sint=\dfrac{1}{2}\int\limits^2_1f\left(t\right)dt+\dfrac{1}{2}\int\limits^3_2f\left(t\right)dt\)
\(=\dfrac{1}{2}\int\limits^2_1\left(t^2-2t+3\right)dt+\dfrac{1}{2}\int\limits^3_2\left(t^2-1\right)dt=\dfrac{23}{6}\)

Đáp án C
Phương pháp:
- Tính vi phân dx theo dt , đổi cận.
- Thay vào tính tìm tích phân và kết luận.
Cách giải:
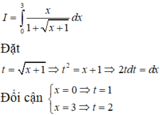
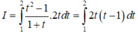
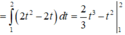
Đối chiếu các đáp án ta thấy A, B, D đúng.
Đáp án C sai vì quên không đổi cận.

Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
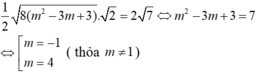
Chọn B.
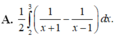
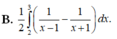
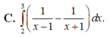
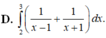
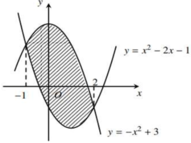
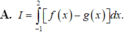
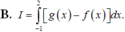
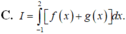
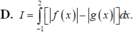
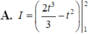
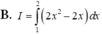
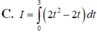
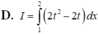
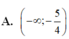

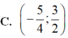
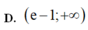
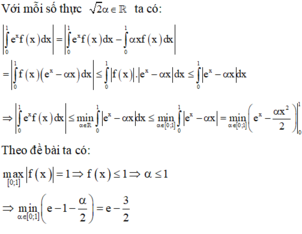

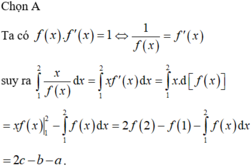
Sử dụng máy tính CASIO
Đáp án B