K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
23 tháng 5 2018
220 = 4. 5. 11 nên ta có các phân số tối giản sau đây thỏa mãn các điều kiện của bài toán:
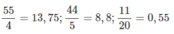

TL
3 tháng 7 2017
gọi p/số tối giản lúc đầu là a/b
nếu chỉ cộng mẫu số ta đc p/s a/a+b , phân số này nhỏ hơn p/số a/b 2 lần
Để a+b/2b gấp 2 lần p/số lúc đầu thì a+b phải = 4 lần
=> mẫu số b phải gấp 3 lần tử số a
=> p/số tối giản thỏa mãn điều kiện đề bài là 1/3
3 tháng 7 2017
- Gọi phân số tối giản cần tìm là : \(\frac{a}{b}\)
Theo đề bài : \(2.\frac{a}{b}=\frac{a+b}{b+b}\)
=) \(\frac{2a}{b}=\frac{a+b}{2b}\)
=) \(\frac{4a}{2b}=\frac{a+b}{2b}\)=) \(4a=a+b\)=) \(3a=b\)
Thay vào phân số cần tìm có dạng : \(\frac{a}{b}=\frac{a}{3a}=\frac{1}{3}\)( Vì \(3a=b\))
Vậy phân số cần tìm là : \(\frac{1}{3}\)
Gọi PS đó là \(\frac{3a}{3b}\)
Vì PS đó lớn hơn 1 nên a>b
Và \(\frac{a}{b}\)là phân số tối giản
UCLN(a,b)=1
Vả lại còn:3a.3b=180
9ab=180
ab=180:9=20
Vậy a=5; b=4 hoặc a=20;b=1 (vì a>b và UCLN(a,b)=1)
Khi đó 3a=15;3b=12 hoặc 3a=60;3b=3
Vậy các PS thỏa mãn là:\(\frac{15}{12},\frac{60}{3}\)