Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
O,I lần lượt là tâm mặt cầu ngoại tiếp hình lập phương và tâm đường tròn đáy của hình trụ ngoại tiếp hình lập phương.
Dễ dàng tính được bán kính mặt cầu ngoại tiếp R 1 = OA = 3 a 2 , bán kính đáy của hình trụ R 2 = 2 a 2 .
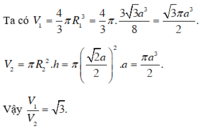

Đáp án là B.
+ Ta có: R C = a 3 ⇒ V C = 4 3 π .3 3 a 3 = 4 π a 3 3 .
+ R T = a 2 ⇒ V T = 2 a .. π 2 a 2 = 4 π a 3
Vậy V C V T = 3 .

Đáp án D
Gọi khối lập phương cần xét ABCD.A'B'C'D' cạnh a.
Bán kính mặt cầu ngoại tiếp khối cầu là R 2 = A A ' 2 = a 2 ⇒ V 1 = 4 3 R 2 3 .
Bán kính mặt cầu ngoại tiếp khối cầu là
R 1 = A C ' 2 = A B 2 + A D 2 + A A ' 2 2 = a 3 2 ⇒ V 1 = 4 3 πR 3 1
Vậy tỉ số k = V 1 V 2 = R 3 1 R 3 1 = R 1 R 2 3 = 3 3 = 3 3 .

Đáp án A.
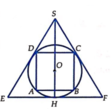
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ S E F đều” (hình vẽ).
Hình vuông ABCD nội tiếp đường tròn (O) nên
A B = B D = 2 R = A B 2 ⇔ A B = 2 R .
⇒ Bán kính đáy và chiều cao của hình trụ (T) lần lượt là r = A B 2 = 2 R 2 và h = A B = 2 R .
Thể tích khối trụ là V T = πr 2 h = π . 2 R 2 2 . 2 R = π 2 R 3 2 .
Ta có ∆ S E F đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của Δ S E F .
Gọi H là trung điểm của EF thì S H = 3 O H = 3 R ⇒ H F = S H . tan 30 ° = R 3
⇒ Bán kính đáy và chiều cao của hình nón (N) lần lượt là H F = R 3 và S H = 3 R . Thể tích khối nón là V N = 1 3 π . HF 2 . SH = 1 3 π R 3 2 . 3 R = 3 πR 3 .
Vậy V T V N = π 2 R 3 2 3 πR 3 = 2 6 .


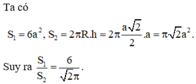
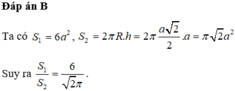

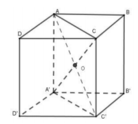


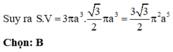
Đáp án A
O, I lần lượt là tâm mặt cầu ngoại tiếp hình lập phương và tâm đường tròn đáy của hình trụ ngoại tiếp hình lập phương.
Dễ dàng tính được bán kính mặt cầu ngoại tiếp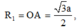
bán kính đáy của hình trụ