Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Bảng phân bố tần số - tần suất
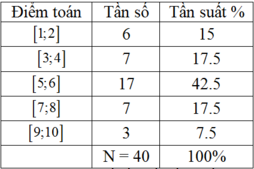
Dựa vào bảng phân bố tần số; tần suất trên ta thấy có 3 lớp có tần suất không bé hơn 17,5% là lớp thứ 2;3 và lớp thứ 4.

Chọn A.
Bảng phân bố tần số - tần suất
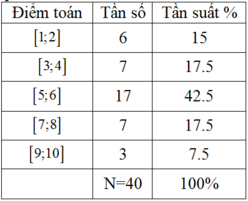
Dựa vào bảng trên ta thấy lớp 3 có tần số và tần suất cao nhất; lớp 5 có tần số; tần suất thấp nhất.
Lớp 2 và 4 có cùng tần số và tần suất.

Chọn B.
Lập bảng phân bố tần số; tần suất
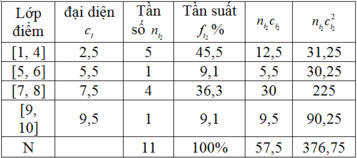
Phương sai của nhóm là
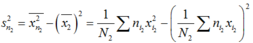
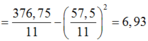

Chọn A.
Lập bảng phân bố tần số; tần suất
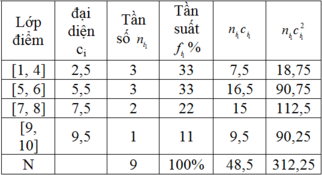
Phương sai của dãy số liệu trên là:
![]()

Chọn A.
Lập bảng phân bố tần số; tần suất
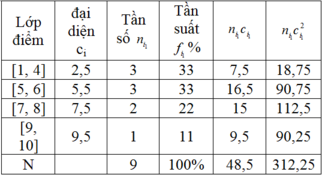
Điểm trung bình cộng của nhóm là:
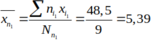

a) Ta có: \(8 - 7 = 1;6 - 7 = - 1;7 - 7 = 0;5 - 7 = - 2;9 - 7 = 2\)
b) +) Bình phương các độ lệch là: \({(8 - 7)^2} = 1;{(6 - 7)^2} = 1;{(7 - 7)^2} = 0;{(5 - 7)^2} = 4;{(9 - 7)^2} = 4\)
+) Trung bình cộng của bình phương các độ lệch là:
\({s^2} = \frac{{{{(8 - 7)}^2} + {{(6 - 7)}^2} + {{(7 - 7)}^2} + {{(5 - 7)}^2} + {{(9 - 7)}^2}}}{5} = 2\)

a) Ta lập bảng tần số:
Điểm | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Tần số | 5 | 13 | 5 | 5 | 5 | 5 | 2 |
Từ đó ta thấy mốt của mẫu số liệu trên là: \({M_o} = 5\)
b) Tỉ lệ số học sinh lớp 10A đạt điểm từ 8 trở lên là: \(\frac{{5 + 5 + 2}}{{40}} = 0,3 = 30\% \)
Tỉ lệ này cho thấy số học sinh đạt điểm giỏi của lớp 10A là \(30\% \)

Chọn D.
Dãy số trên đã được sắp xếp theo thứ tự tăng dần.
Dãy số trên có 9 phần tử. Trong dãy này số đứng giữa là 7.
⇒ Số trung vị là 7.

a) * Lớp 10C:

* Lớp 10D:

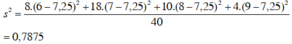
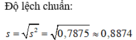
b) Kết quả lớp 10D có độ lệch chuẩn nhỏ hơn kết quả lớp 10C nên kết quả lớp 10D đồng đều hơn.
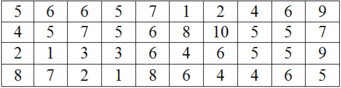
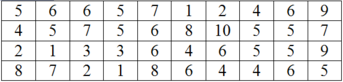
+ Các giá trị khác nhau: x 1 = 3 , x 2 = 4 , x 3 = 5 , x 4 = 6 , x 5 = 7 , x 6 = 8 , x 7 = 9 , x 8 = 10 ⇒ A đúng.
+ Giá trị x7 = 9 xuất hiện 6 lần ⇒ Tân số là 6 ⇒ B đúng.
+ Giá trị x8= 10 xuất hiện 4 lần ⇒ Tần suất là 4 10 hay 10 % ⇒ C đúng ⇒ D sai.
Đáp án D.