Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các công thức lần lượt là:
♦ \(a^m.a^n=a^{m+n}\)
♦ \(a^m:a^n=a^{m-n}\)
♦ \(\left(a^m\right)^n=a^{m.n}\)
♦ \(\left(m.n\right)^a=m^a.n^a\)
♦ \(\left(\dfrac{m}{n}\right)^a=\dfrac{m^a}{n^a}\)
Lần lượt :
a) am.an = am+n
b) am : an = am-n (m≥n , a≠0)
c) (an)m = am.n
d) (a.b)m = am.bm
e- (\(\dfrac{a}{b}\))m = \(\dfrac{^{a^m}}{b^m}\)

1. Viết công thức:
- Nhân hai lũy thừa cùng cơ số: tổng 2 số mũ
xm . xn = xm+n
- Chia hai lũy thừa cùng cơ số: hiệu 2 số mũ
xm : xn = xm - n (x # 0, lớn hơn hoặc bằng n)
- Lũy thừa của 1 lũy thừa: Tích 2 số mũ
(xm )n = xm.n
- Lũy thừa của một tích: tích các lũy thừa
(x . y)n = xn . yn
- Lũy thừa của một thương: thương các lũy thừa
2. Thế nào là tỉ số của hai số hữu tỉ ? Cho ví dụ
- Số hữu tỉ là số viết đc dưới dạng phân số \(\frac{a}{b}\)
Vd: \(\frac{3}{4}\); 18

Nếu một số phân tích ra thành tích các thừa số nguyên tố:a=pt11.pt22...ptkk
thì số các số là ước của số a sẽ là (p1+1)(p2+1)...(pk+1)
Dựa vào nhận xét này, ta suy ra để số a là nhỏ nhất ta suy ra các thừa số nguyên tố có trong phân tích của số a phải là các thừa số từ nhỏ nhất đến lớn nhất có thể
Nhận xét thứ hai là với số có 16 ước ta có các trường hợp sau:
16=1.16=2.8=4.4=2.2.4=2.2.2.2
Với trường hợp 16 = 1.16 thì khi đó số a có dạng là a=\(2^{15}\)=32768
Với trường hợp 16 = 2.8 thì số a khi đó số a có dạng là a=\(2^7.3^1\)=384
Với trường hợp 16 = 4.4 thì khi đó số a có dạng là a=\(2^3.3^3\)=216
Với trường hợp 16 = 2.2.4 thì khi đó số a có dạng là a=\(2^3.3^2.5^1\)=120
Với trường hợp 16 = 2.2.2.2 thì khi đó số a có dạng là a=\(2^1.3^1.5^1.7^1\)=210
Bằng lập luận toán học ta vẫn có thể suy ra số a là 120
Bài toán trở thành tìm chữ số tận cùng của \(92^{120}\)
Ta dễ dàng có được: \(92^{120}=92^{4.30}=\left(92^4\right)^{30}=\left(....6\right)^{30}=...6\)
Chúc bạn học tốt

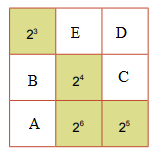
Ta đặt các ô chưa biết như sau:
Ta có:
Tích của mỗi hàng, cột, đường chéo bằng: \({2^3}{.2^4}{.2^5} = {2^{3 + 4 + 5}} = {2^{12}}\)
\(\begin{array}{l}A = {2^{12}}:{2^6}:{2^5} = {2^{12 - 6 - 5}} = {2^1} = 2;\\B = {2^{12}}:{2^1}:{2^3} = {2^{12 - 1 - 3}} = {2^8};\\C = {2^{12}}:{2^8}:{2^4} = {2^{12 - 8 - 4}} = {2^0} = 1;\\D = {2^{12}}:{2^0}:{2^5} = {2^{12 - 0 - 5}} = {2^7};\\E = {2^{12}}:{2^7}:{2^3} = {2^{12 - 7 - 3}} = {2^2}\end{array}\)
Vậy ta có bảng hoàn chỉnh là:


a) ta có: x10 : x7 = x3
=> tích đó đc viết là: x7 * x3
b) ta có: x2 * 5 = x10
=> lũy thừa của x^2 đc viết là: (x2)5
c) ta có: x12 : x10 = x2
=> thương của 2 lũy thừa trong đó số bị chia là x12 đc viết là: x12 : x2
mk biết kết quả nhưng trình bày ko biết đúng ko?
a) \(x^7\cdot x^3=x^{10}\)
b)\(\left(x^2\right)^5=x^{10}\)
c)\(^{x^{12}:x^2=x^{10}}\)

Ta có:
\(\begin{array}{l}{3^0}{.3^1} = {3^{0 + 1}} = {3^1};\\{3^1}{.3^1} = {3^{1 + 1}} = {3^2};\\{3^1}{.3^2} = {3^{1 + 2}} = {3^3};\\{3^2}{.3^3} = {3^{2 + 3}} = {3^5};\\{3^3}{.3^5} = {3^{3 + 5}} = {3^8}\end{array}\)
Vậy ta được: