Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
t1 = 345oC
c1 = 460J/KgK
m2 = 3kg
t2 = 25oC
c2 = 4200J/KgK
to = 33oC
m1 = ?
------------------------------------
Nhiệt lượng thu vào của nước là:
Qthu = \(m_1\cdot c_1\cdot\left(t^o-t_2\right)\)
= \(3\cdot4200\cdot\left(33-25\right)\)
= 100800 (J)
Theo phương trình cân bằng nhiệt:
Qthu = Qtỏa = 100800J
Qtỏa = \(m_1\cdot c_1\cdot\left(t_1-t^o\right)\)
100800J = \(m_1\cdot460\cdot\left(345-33\right)\)
=> m1 = \(\dfrac{100800}{460\cdot\left(345-33\right)}\) = 0,7 (kg)

Sau khi cân bằng, nhiệt độ của thép chính là nhiệt độ của nước
=> tthép = 30oC
Nhiệt độ ban đầu của thép là t = 7 độ C
Giải thích các bước giải:
Nhiệt lượng miếng thép toả ra khi nguội đi: Q = mc(345 - 30) = 2.460.315 = 289 800J
Goij nhiệt độ ban đầu của nước là t
Nhiet lượng nước thu vào là
Q' = m'.c'(30 - t) = 3.4200(30 - t) = 12600(30 - t)
Ta có Q = Q' nên 12600(30 - t) = 289 800
Giải ta được t = 7

Ta có phương trình cân bằng nhiệt
\(Q_{toả}=Q_{thu}\\ m_1c_1\Delta t=m_2c_2\Delta t\\ \left(1,2.460\right)\left(85-t_{cb}\right)=2.4200\left(t_{cb}-32\right)\\ \Rightarrow t_{cb}\approx35^o\)

a) Nhiệt độ của miếng nhôm ngay khi có cân bằng nhiệt là 27oC.
b) Nhiệt lượng do quả cầu tỏa ra
Q1 = m1C1(t1 –t) = 0,2.880.(100 – 27) = 12848J
c) Nhiệt lượng do nước thu vào để tăng nhiệt độ đến 27oC
Q2 = m2C2(t-t2) = m2.4200.(27-20) = \(29400.m_2\)
Áp dụng phương trình cân bằng nhiệt, ta có:
Q1 = Q2 => 12848= \(29400.m_2\)
m2 =\(\frac{12848}{29400}=0,44kg\)
Vậy khối lượng của nước là 0,44kg.

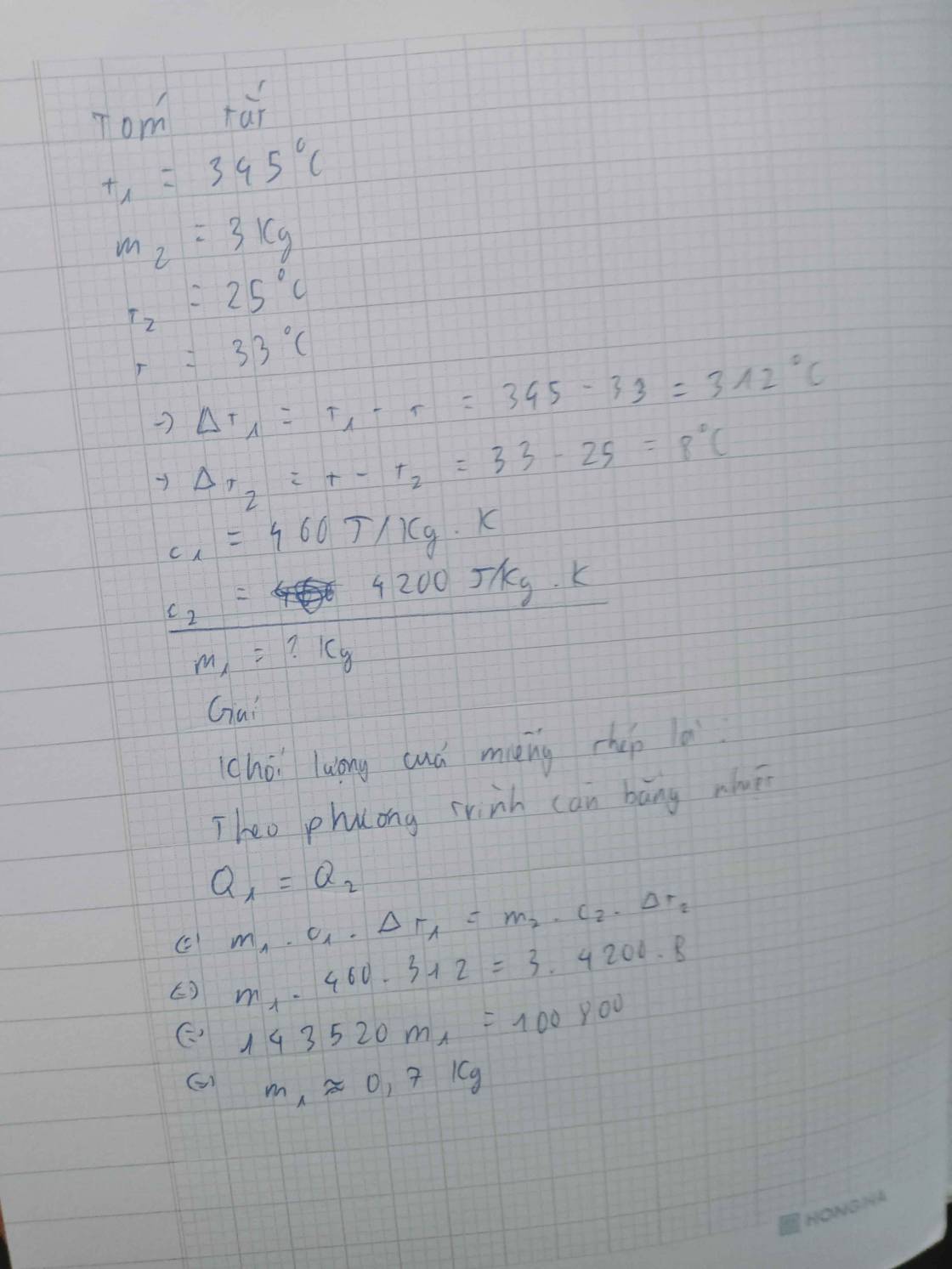

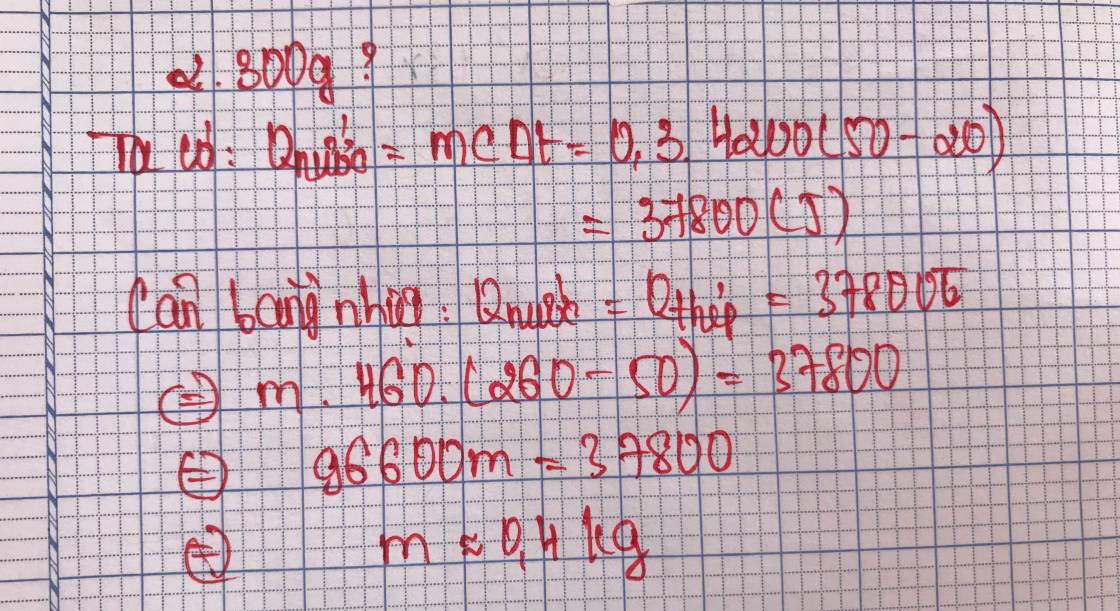

3 lít nước = 3 kg
Gọi nhiệt độ ban đầu của nước là t 0
- Nhiệt lượng của miếng thép tỏa ra là:
Q 1 = m 1 c 1 ∆ t 1 = 2.460.(345 – 30) = 289800 J
- Nhiệt lượng mà nước thu vào là:
Q 2 = m 2 c 2 ∆ t 2 = 3.4200.(30 – t0)
- Áp dụng phương trình cân bằng nhiệt, ta có:
Q 1 = Q 2 ⇔ 289900 = 3.4200.(30 – t 0 )
⇒ t 0 = 7 o C
⇒ Đáp án A