K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
19 tháng 6 2017
t 2
Ta có: x + y + x y = - 13 x 2 + y 2 - x - y = 32 ⇔ x + y + x y = - 13 ( x + y ) 2 - 2 x y - ( x + y ) = 32
Đặt S = x+ y; P = xy . Khi đó, hệ phương trình trên trở thành:
S + P = - 13 ( 1 ) S 2 - 2 P - S = 32 ( 2 )
Từ (1) suy ra: P = -S – 13 thay vào (2) ta được:
S 2 – 2(-S – 13) – S = 32
⇔ S 2 + 2 S + 26 - S - 32 = 0 ⇔ S 2 + S - 6 = 0 ⇔ [ S = 2 S = - 3
* Với S = 2 thì P = -15 . Khi đó , x và y là nghiệm phương trình:
t 2 - 2t – 15 = 0 ⇔ [ t = 5 t = - 3
* Với S = -3 thì P = -10. Khi đó, x và y là nghiệm phương trình:
t 2 + 3t – 10 =0 ⇔ [ t = 2 t = - 5
Vậy hệ phương trình đã cho có 4 nghiệm ( 5; -3); (-3; 5); (2; -5); (-5; 2).
Chọn D.
CM
29 tháng 12 2017
Trừ vế cho vế phương trình (1) cho (2) ta được:
x 2 + y 2 − y = − 1 ⇔ x 2 + y 2 − y + 1 = 0
Ta có:
x 2 ≥ 0 , ∀ x y 2 − y + 1 = y − 1 2 2 + 3 4 > 0 , ∀ y ⇒ x 2 + y 2 − y + 1 > 0 , ∀ x , y
Do đó phương trình x 2 + y 2 − y + 1 = 0 vô nghiệm
Vậy không tồn tại giá trị của xy
Đáp án cần chọn là: D
CM
10 tháng 6 2017
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12
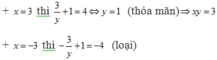
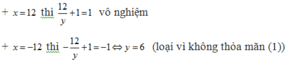
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
CM
13 tháng 4 2019
Phương trình 1 ⇔ x + y 2 x - y = 0 ⇔ x = − y 2 x = y
Trường hợp 1: x = - y thay vào (2) ta được x 2 - 4 x + 3 = 0 ⇔ x = 1 x = 3
Suy ra hệ phương trình có hai nghiệm là (1; −1), (3; −3).
Trường hợp 2: 2 x = y thay vào (2) ta được - 5 x 2 + 17 x + 3 = 0 phương trình này không có nghiệm nguyên.
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; −1) và (3; −3).
Đáp án cần chọn là: C
CM
14 tháng 4 2018
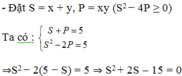
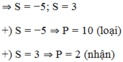
Khi đó: x, y là nghiệm của phương trình X 2 - 3 X + 2 = 0 ⇔ X = 1 ; X = 2
Vậy hệ có nghiệm (2; 1), (1; 2)
Đáp án cần chọn là: C
CM
15 tháng 10 2017
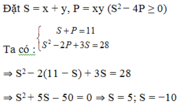
Khi S = 5 ⇒ P = 6 thì x, y là nghiệm của phương trình
Khi S = −10 ⇒ P = 21 thì x, y là nghiệm của phương trình
Vậy hệ có nghiệm (3; 2), (2; 3), (−3; −7), (−7; −3).
Đáp án cần chọn là: D
PT
1
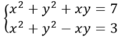
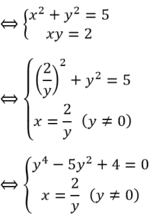
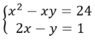
@Lê Nhật Anh nhầm chỗ \(a^2-\left(2-a\right)=4\)
\(\Rightarrow a^2+a-6=0\)
\(\left\{{}\begin{matrix}x+xy+y=2\\x^2+y^2+xy=4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x+y+xy=2\\\left(x+y\right)^2-xy=4\end{matrix}\right.\)
Đặt \(x+y=a;xy=b\)
Hệ trở thành: \(\left\{{}\begin{matrix}a+b=2\\a^2-b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2-a\\a^2-\left(2-a\right)=4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}b=2-a\\a^2+a-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2-a\\\left(a-1\right)\left(a+2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\\\left\{{}\begin{matrix}a=-2\\b=4\end{matrix}\right.\end{matrix}\right.\)
+)\(\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\xy=1\end{matrix}\right.\)
\(\Rightarrow\) \(x,y\) là hai nghiệm của phương trình \(X^2-X+1=0\)( vô nghiệm)
+) \(\left\{{}\begin{matrix}a=-2\\b=4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x+y=-2\\xy=4\end{matrix}\right.\)
\(\Rightarrow\)\(x,y\) là hai nghiệm của phương trình \(Y^2+2Y+4=0\)( vô nghiệm)
Vậy hệ phương trình vô nghiệm