Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt độ dài 2 cạnh góc vuông của tam giác đó là a và b; độ dài cạnh huyền là c (a,b,c > 0)
Diện tích của tam giác đó là \(\frac{ab}{2}=14\)(cm2) \(\Rightarrow ab=28\Leftrightarrow2ab=56\)(1)
Áp dụng ĐL Pytago ta có: \(a^2+b^2=c^2=13^2=169\)(2)
(1) + (2) \(\Rightarrow a^2+2ab+b^2=56+169=225\Leftrightarrow\left(a+b\right)^2=225\)
\(\Leftrightarrow a+b=\sqrt{225}=15\)(cm). Vậy ...

Gọi H là trung điểm của BC
=> AH là đường trung tuyến của tam giác ABC vuông cân tại A
=> AH là đường cao của tam giác ABC vuông cân tại A
AH = \(\frac{BC}{2}\) = \(\frac{a}{2}\)
SABC = \(\frac{AH\times BC}{2}=\frac{\frac{a}{2}\times a}{2}=\frac{a^2}{2}\times2=a^2\)

Áp dụng định lý Pitago vào tam giác đó ta có:
\(13^2=a^2+b^2\)(1)
\(\frac{1}{2}ab=14=>ab=28\)(2)
Từ 1 và 2 => \(a^2+2ab+b^2=169+56=225\)
Nên áp dụng hđt ta có : \(\left(a+b\right)^2=225\\ a+b=15\)
Ta co Sabc=1/2ab hay 14 =1/2ab suy ra ab=28
Theo dinh ly pytago ta co a^2+b^2=13^2 hay (a+b)^2-2ab=13^22
Ban thay so vao tinh tiep nhe mijh ko mag may tinh

Gọi độ dài cạnh góc vuông của tam giác vuông cân là a (0 < a < l)
Áp dụng định lí Pi-ta-go vào tam giác vuông ta có:
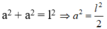
Diện tích tam giác vuông đó là:
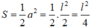

Diện tích tam giác vuông là:
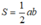
trong đó a,b là độ dài 2 cạnh góc vuông
Suy ra:
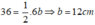
Cạnh huyền của tam giác vuông là:
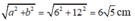
Chọn đáp án B
Ta có diện tích của tam giác: S = 1/2a.h.
Trong đó: a là độ dài cạnh đáy, h là độ dài đường cao
Chọn đáp án C.