Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: AD=HE => AD+DH=HE+DH => AH=DE => AH2=DE2; AD=HE => AD2=HE2.
AH vuông góc BC => Tam giác BHE vuông tại H => BE2=BH2+HE2 (Định lí Pytago) (1)
AH vuông góc BC, DF//BC => DF vuông góc với AH => Tam giác EDF vuông tại D => EF2=DE2+DF2 (Pytago) (2)
Từ (1) và (2) => BE2+EF2=BH2+HE2+DE2+DF2 (3)
Thay AH2=DE2; AD2=HE2 (cmt) vào (3), ta được: BE2+EF2=BH2+AD2+AH2+DF2 => BE2+EF2=(BH2+AH2)+(AD2+DF2)
=> BE2+EF2=AB2+AF2 (Áp dụng định lí Pytago với 2 cặp cạnh)
Xét tam giác ABF có: ^A=900 => AB2+AF2=BF2, thay vào biểu thức trên ta có: BE2+EF2=BF2.
=> Tam giác BEF có: BE2+EF2=BF2 => Tam giác BEF vuông tại E (Định lí Pytago đảo) (đpcm).
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
b: Xét ΔABD có
AH vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
=>tan ADH=tan ABD=tan ABC=AC/AB=4/3
Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC=HD*HC
Gọi AM cắt DE tại I
Theo tính chất hình chữ nhật ADHE : \(\widehat{E_1}=\widehat{HAC}=\widehat{MBA};\widehat{A_1}=\widehat{D_1}=\widehat{AHE}=\widehat{MCA}\)
\(\Rightarrow\widehat{A_1}=\widehat{ACM}\Rightarrow\Delta ACM\)cân tại M \(\Rightarrow MA=MC\)(*)
Do \(\Delta AID\)vuông tại I suy ra
\(\widehat{DAM}+\widehat{D_1}=90^0\Leftrightarrow\widehat{DAM}+\widehat{DAH}=90^0\left(1\right)\)
\(\widehat{ABM}+\widehat{DAH}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{DAM}=\widehat{ABM}\)
\(\Rightarrow\Delta ABM\)cân tại M \(\Rightarrow MA=MB\)(**)
Từ (*);(**) suy ra MB=MC hay M là trung điểm BC . Do MF//AC suy ra
\(\widehat{MFC}=\widehat{ACF}\)
Mà
\(\widehat{ACF}=\widehat{MCF}\Rightarrow\widehat{MFC}=\widehat{MCF}\Rightarrow\Delta MFC\)cân tại M suy ra MC=MF
Mà MB=MC suy ra 
\(\Delta BFC\) có FM là trung tuyến 
\(FM=\frac{1}{2}BC\Rightarrow\) \(\Delta BFC\)vuông tại F hay 
\(BF\perp CF\left(đpcm\right)\)
GIẢI: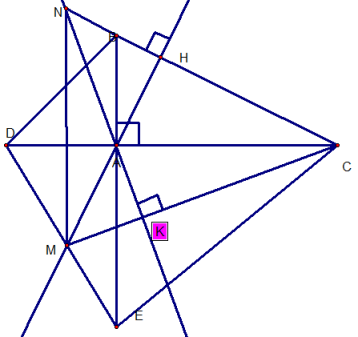
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
làm giúp mik với
Gợi ý: EF // BC => EF vuông AH
Áp dụng định lí Pitago
\(BE^2=AB^2+BE^2=BD^2+DE^2\)
=> \(\left(BH^2+AH^2\right)+\left(AF^2+FE^2\right)=\left(BH^2+HD^2\right)+\left(EF^2+FD^2\right)\)
=> \(HA^2+AF^2=HD^2+FD^2\)
=> \(\left(AF+FH\right)^2+AF^2=HD^2+\left(HD+FH\right)^2\) ( dùng hằng đẳng thức và rút gọn)
=> \(AF^2+AF.FH=HD^2+HD.FH\)
=> \(\left(AF^2-HD^2\right)+FH\left(AF-HD\right)=0\)
=> AF=HD