
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Do \(\Delta ABH\)vuông (gt):
mà I Trung điểm AB (gt)
nên \(HI=\frac{1}{2}AB=\frac{6}{2}=3cm\)
b) Xét Tứ giác AHBK:
HI = HK (gt)
AI = AB (gt)
=> Tứ giác ABHK là hình bình hành (2 đường chéo cắt nhau tai trung điểm mỗi đường)
mà \(HI=\frac{1}{2}AB\Leftrightarrow2HI=AB\Leftrightarrow HK=AB\)
=> Hình bình hành ABHK là hình chữ nhật (đpcm).
c) Điều kiện để HCN ABHK là hình vuông thì \(\Delta ABC\)thì:
Dường cao AH = HB
=> HCN AHBK là hình vuông.

a: Xét tứ giác AHBK có
M là trung điểm của AB
M là trung điểm của HK
Do đó: AHBK là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBK là hình chữ nhật
b:
Xét tứ giác AKHC có
AK//HC
AK=HC
Do đó: AKHC là hình bình hành
c: Xét ΔABC có
N là trung điểm của AC
H là trung điểm của BC
Do đó: NH là đường trung bình
=>NH//AB và NH=AB/2
hay NH//AM và NH=AM
=>AMHN là hình bình hành
mà AM=AN
nên AMHN là hình thoi

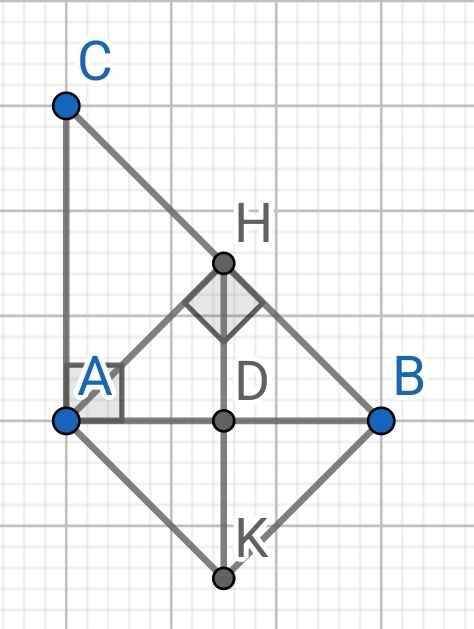
Do AH ⊥ BC (gt)
⇒ AH ⊥ BH
Do ∆ABC vuông cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Gọi D là giao điểm của AB và HK
Do H và K đối xứng nhau qua AB (gt)
⇒ D là trung điểm của HK và AB là đường trung trực của HK
⇒ HK ⊥ AB
Mà AB ⊥ AC
⇒ HK // AC
⇒ HD // AC
Mà H là trung điểm của BC
⇒ D là trung điểm AB
Do ∆ABC vuông cân tại A (gt)
AH là đường trung tuyến của ∆ABC (cmt)
⇒ AH = HB = HC = BC : 2
Tứ giác AHBK có:
D là trung điểm HK (cmt)
D là trung điểm AB (cmt)
⇒ AHBK là hình bình hành
Mà AH ⊥ BH (cmt)
⇒ AHBK là hình chữ nhật
Lại có AH = BH (cmt)
⇒ AHBK là hình vuông

a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: ADHE là hình chữ nhật
nen AH=DE
c: Để ADHE là hình vuông thì AH là phân giác của góc DAE
=>ΔABC cân tại A
=>AB=AC