Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

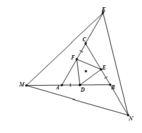
a) Ta có: \(\Delta ABC\) đều (gt) (1).
\(\Rightarrow AB=BC=AC\) (tính chất tam giác đều).
Mà \(AD=BE=CF\left(gt\right)\)
\(\Rightarrow AB-AD=BC-BE=AC-CF.\)
\(\Rightarrow BD=CE=AF.\)
Từ (1) \(\Rightarrow\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60^0\) (tính chất tam giác đều).
Hay \(\widehat{DAF}=\widehat{EBD}=\widehat{FCE}=60^0.\)
Xét 3 tam giác \(ADF;BED\) và \(CFE\) có:
\(AD=BE=CF\left(gt\right)\)
\(\widehat{DAF}=\widehat{EBD}=\widehat{FCE}\left(cmt\right)\)
\(AF=BD=CE\left(cmt\right)\)
=> \(\Delta ADF=\Delta BED=\Delta CFE\left(c-g-c\right)\)
=> \(DF=ED=FE\) (các cạnh tương ứng).
=> \(\Delta DEF\) là tam giác đều.
Chúc bạn học tốt!

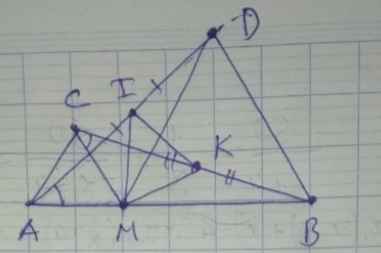
a) Ta có: \(\widehat{AMD}=\widehat{AMC}+\widehat{CMD}\)
\(=60^0+\widehat{CMD}\) \(\left(1\right)\)
Lại có: \(\widehat{CMB}=\widehat{BMD}+\widehat{CAD}\)
\(=60^0+\widehat{CMD}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\): ⇒ \(\widehat{AMD}=\widehat{CMB}\)
Xét △ AMD và △ CMB có:
CH = AM ( △ AMC đều )
\(\widehat{AMD}=\widehat{CMB}\) ( cmt )
MB = MD ( △ BMD đều )
⇒ △ AMD = △ CMB ( c - g - c )
Do đó: AD = CB ( 2 cạnh tương ứng )
b) Ta có: \(CK=\dfrac{BC}{2}\) ( K là trung điểm CB )
Ta có: \(AI=\dfrac{AD}{2}\) ( I là trung điểm AD )
Mà BC = AD ( cmt ) ⇒ CK = AI
Xét △ AMI và △ CMK có:
CM = AM ( △ AMC đều )
\(\widehat{IAM}=\widehat{KCM}\) ( vì △ AMD = △ CMB )
AI = CK ( cmt )
⇒ △ AMI = △ CMK ( c - g - c )
⇒ MK = MI
⇒ △ IMK cân tại M

a: Xét ΔAMB và ΔKMC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)
MB=MC
Do đó: ΔAMB=ΔKMC
b: Xét tứ giác BECF có
BE//CF
BE=CF
Do đó: BECF là hình bình hành
Suy ra: BC và EF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của FE
hay F,M,E thẳng hàng

Xét ΔBDE và ΔAFD có
BE=AD
góc EBD=góc DAF
AF=BD
=>ΔBDE=ΔAFD
=>DE=FD
Xét ΔBDE và ΔCEF có
BE=CF
góc DBE=góc ECF
BD=CE
=>ΔBDE=ΔCEF
=>DE=EF=FD
=>ΔDEF đều