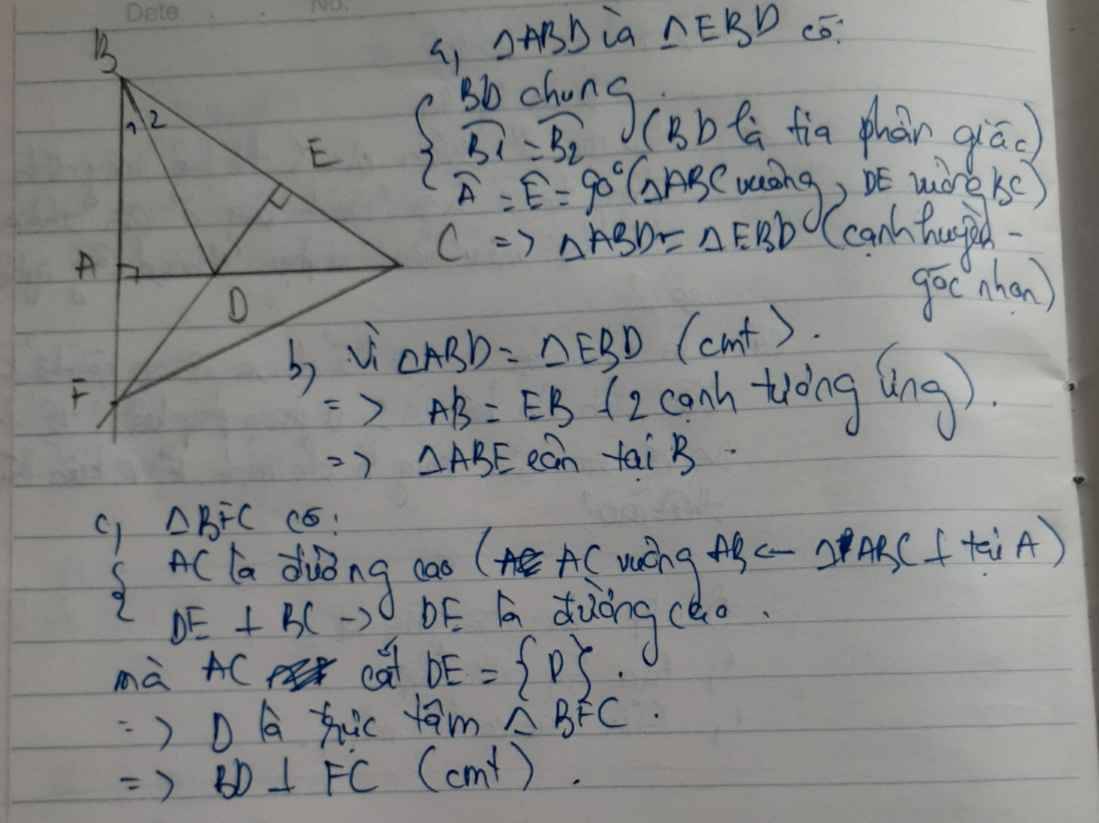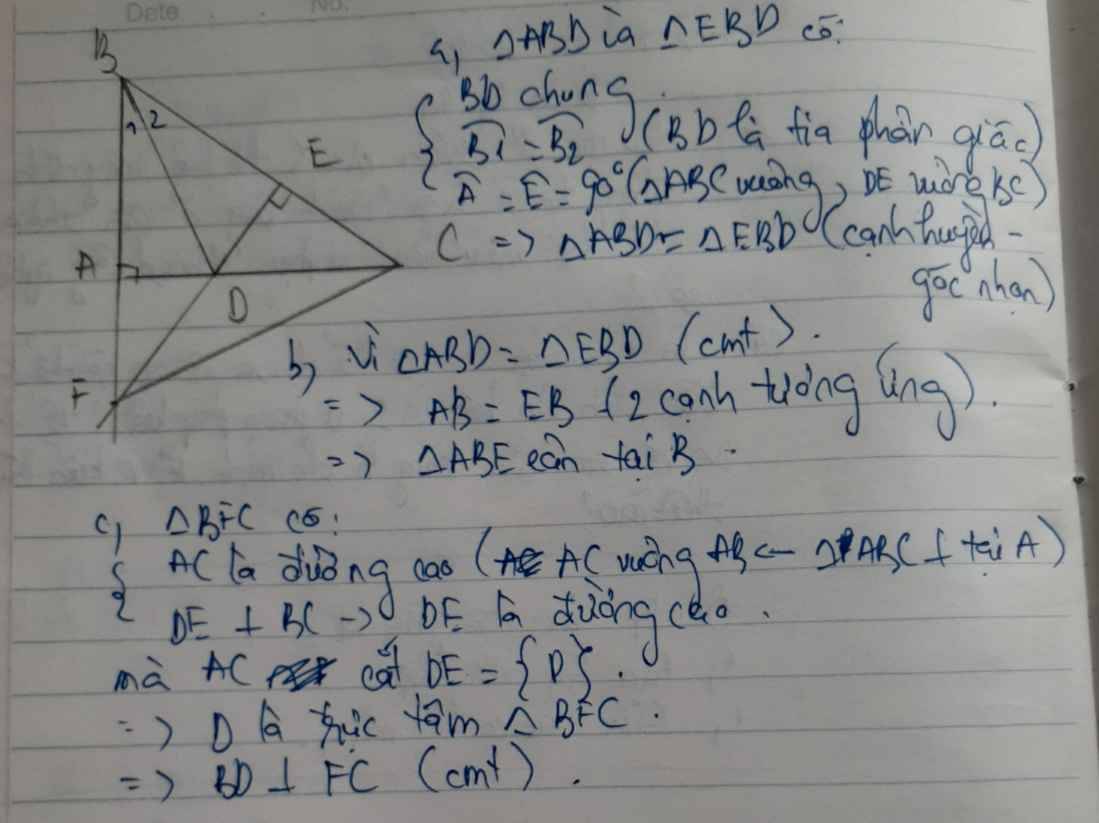Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sao nhiều bạn biết làm mà không giúp bạn này z
chắc bạn ấy đang cần gấp lắm á, giúp bạn ấy di nào!!!
a) Xét ∆ABD và ∆ACD, ta có
AB=AC(GT)
<ABD=<ACD=90°
AD cạnh chung
⟹ ∆ABD=∆ACD(c.h-cgv) ⟹<BAD=<CAD( 2 góc tương ứng)
Xét ∆ABC và ∆ACD, ta có:
AB=AC(GT)
<BAD=<CAD(CMT)
AC cạnh chung
⟹ ∆ABC=∆ACD (c.g.c)
b) Ta có : BD=DC(Vì ∆ABD=∆ACD (CM ở a)) <1>
BC=DC( Vì ∆ABC=∆ACD(CM ở a)) <2>
Từ <1> và <2>
⟹ BD=DC=BC
⟹ ∆BDC là tam giác đều
c) Ta có: AD>BD(Vì AD là cạnh huyền tương ứng của tam giác vuông ABD)
BC=BD( Vì ∆BDC là tam giác đều (CM ở b))⟹2BC>BD
⟹ 2BC=+AD>AB+BD

a) Xét t/g ABD và t/g HBD có:
AB = BH (gt)
ABD = HBD ( vì BD là phân giác ABC)
BD là cạnh chung
Do đó, t/g ABD = t/g HBD (c.g.c)
=> BAD = BHD = 90o (2 góc tương ứng)
=> DH _|_ BC (đpcm)
b) t/g ABD = t/g HBD (câu a)
=> ADB = HDB (2 góc tương ứng)
Mà ADB + HDB = ADH = 110o
Do đó, ADB = HDB = 110o : 2 = 55o
t/g ABD vuông tại A có: ABD + ADB = 90o
=> ABD + 55o = 90o
=> ABD = 90o - 55o = 35o
k nhé

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó; ΔABD=ΔACD
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD

a) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(Cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)
b) Ta có: \(\widehat{BDA}+\widehat{DAH}=90^0\)
\(\widehat{BAD}+\widehat{KAD}=90^0\)
mà \(\widehat{DAH}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
nên \(\widehat{BDA}=\widehat{BAD}\)
Xét ΔABD có \(\widehat{BDA}=\widehat{BAD}\)(cmt)
nên ΔABD cân tại B(Định lí đảo của tam giác cân)
c) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)

a: Xét ΔABD vuông tại B và ΔAED vuông tại E có
AD chung
góc BAD=góc EaD
=>ΔBAD=ΔEAD
b: ΔBAD=ΔEAD
=>AB=AE
=>ΔABE cân tại A
mà góc BAE=60 độ
nên ΔABE đều