Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow ab\left(\dfrac{1}{b+c}-\dfrac{1}{a+c}\right)+bc\left(\dfrac{1}{a+c}-\dfrac{1}{a+b}\right)+ca\left(\dfrac{1}{a+b}-\dfrac{1}{b+c}\right)=0\)
\(\Leftrightarrow\dfrac{ab\left(a-b\right)}{\left(b+c\right)\left(a+c\right)}+\dfrac{bc\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{ca\left(c-a\right)}{\left(a+b\right)\left(b+c\right)}=0\)
\(\Leftrightarrow\dfrac{ab\left(a^2-b^2\right)+bc\left(b^2-c^2\right)+ca\left(c^2-a^2\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
\(\Leftrightarrow\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)\left(a+b+c\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\) hay tam giác cân

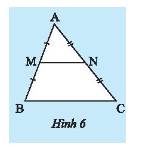
a) Vì \(AM = MB \Rightarrow M\) là trung điểm của \(AB\) (do \(M\) thuộc \(AB\))
\( \Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\);
Vì \(AN = NC \Rightarrow N\) là trung điểm của \(AC\) (do \(N\) thuộc \(AC\))
\( \Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}\).
b) Vì \(\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên áp dụng định lí Thales đảo ta được \(MN//BC\).
c) Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng hệ quả định lí Thales ta được \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\).
Vậy \(\frac{{MN}}{{BC}} = \frac{1}{2}\) (điều phải chứng minh).

Mình không biết vẽ hình khi trả lời nên bạn tự vẽ nhé
Đầu tiên chứng minh \(NE=\frac{1}{6}AN\)
Qua E kẻ đường thẳng song song BF cắt AC tại K
Theo ta-lét ta có:
\(\frac{FK}{FC}=\frac{BE}{BC}=\frac{1}{3}\)=>\(\frac{FK}{ÀF}=\frac{1}{6}=\frac{NE}{AN}\)
Từ E,N,C kẻ các đường cao tới AB lần lượt là H,G,I
Theo talet ta có
\(\frac{EH}{CI}=\frac{BE}{BC}=\frac{1}{3},\frac{NG}{EH}=\frac{AN}{AE}=\frac{6}{7}\)
=> \(\frac{NG}{CI}=\frac{2}{7}\)=> \(\frac{NG.AB}{CI.AB}=\frac{2}{7}\)
=> \(\frac{S_{ABN}}{S_{ABC}}=\frac{2}{7}\)
Tương tự \(\frac{S_{BPC}}{S_{ABC}}=\frac{2}{7}\),\(\frac{S_{AMC}}{S_{ABC}}=\frac{2}{7}\)
=> \(S_{MNP}=S_{ABC}-S_{AMC}-S_{ABN}-S_{BCP}=\frac{1}{7}S_{ABC}\)
Vậy \(S_{MNP}=\frac{1}{7}S_{ABC}\)