Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

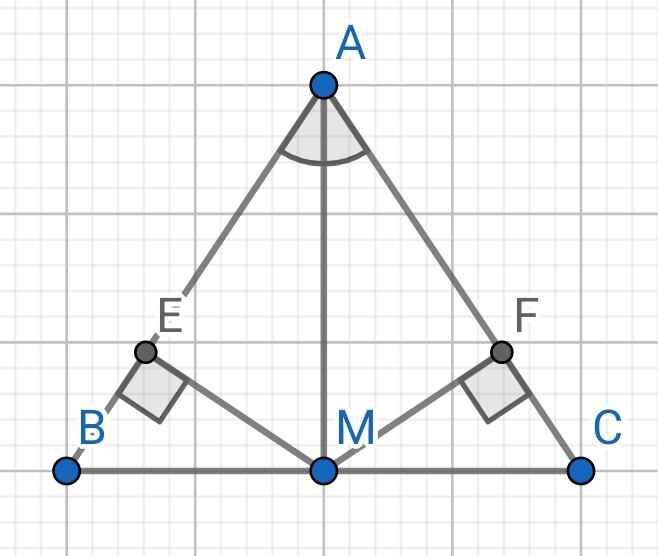
Cho △ABC có AB = AC, AM là phân giác của ∠BAC (M ∈ BC):
a, Chứng minh △ABM = △ACM.
b, Chứng minh M là trung điểm của BC và AM ⊥ BC.
c, Kẻ MF ⊥ AB (F ∈ AB) và ME ⊥ AC (E ∈ AC). Chứng minh EF // BC.
Giải:
a,
- Xét 2 △ABM và △ACM, có:
AB = AC (theo giả thiết)
∠CAM = ∠BAM (AM là phân giác của ∠BAC)
AM_cạnh chung
=> △ABM = △ACM (c.g.c)
b,
- Có △ABM = △ACM (chứng minh trên)
=> MC = MB (2 cạnh tương ứng)
=> M là trung điểm của BC
=> ∠AMC = ∠AMB (2 góc tương ứng)
mà 2 ∠AMC và ∠AMB kề bù
=> ∠AMC = ∠AMB = \(\dfrac{180^o}{2}\) = 90o
<=> AM ⊥ BC
c,
- Xét 2 △AEM và △AFM, có:
∠AEM = ∠AFM = 90o
AM_cạnh chung
∠EAM = ∠FAM (AM là phân giác của ∠EAF)
=> △AEM = △AFM (cạnh huyền - góc nhọn)
=> AE = AF (2 cạnh tương ứng)
<=> △AEF cân tại A
=> ∠AEF = \(\dfrac{180^o-\text{∠}EAF}{2}\) (số đo của một góc ở đáy trong △AEF cân tại A) (1)
Có △ABC cân tại A (AB = AC)
=> ∠ACB = \(\dfrac{180^o-\text{∠}BAC}{2}\) (số đo của một góc ở đáy trong ΔABC cân tại A) (2)
Từ (1) và (2) suy ra ∠AEF = ∠ACB
mà ∠AEF và ∠ACB ở vị trí đồng vị
=> EF//BC

 a) Do AM là tia phân giác của ∠BAC (gt)
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)

a: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó:ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó:ΔAEM=ΔAFM
Suy ra:ME=MF
hay ΔMEF cân tại M
c: Ta có: AE=AF
ME=MF
Do đó: AM là đường trung trực của FE
hay AM⊥FE

a, Xét tam giác AMB và tam giác AMC có
AM _ chung
AB = AC
^MAB = ^MAC
Vậy tam giác AMB = tam giác AMC (c.g.c)
b, Xét tam giác AEM và tam giác AFM có
AM _ chung
^MAE = ^MAF
Vậy tam giác AEM = tam giác AFM (ch-gn)
=> AE = AF ( 2 cạnh tương ứng )
=> EM = FM ( 2 cạnh tương ứng )
Xét tam giác MEF có EM = FM
Vậy tam giác MEF cân tại M
c, AE/AB = AF/AC => EF // BC
mà tam giác ABC cân tại A có AM là phân giác
đồng thời là đường cao
=> AM vuông BC
=> AM vuông EF

a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{BAM}=\widehat{CAM}\)
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>ME=MF
=>ΔMEF cân tại M
c: ta có: ΔAEM=ΔAFM
=>AE=AF
=>A nằm trên đường trung trực của EF(1)
ta có: ME=MF
=>M nằm trên đường trung trực của EF(2)
Từ (1) và (2) suy ra AM là đường trung trực của EF
=>AM\(\perp\)EF
d: Kẻ FH\(\perp\)BC
Ta có: AE+EB=AB
AF+FC=AC
mà AE=AF và AB=AC
nên EB=FC
Xét ΔEIB vuông tại I và ΔFHC vuông tại H có
EB=FC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔEIB=ΔFHC
=>EI=FH và BI=CH
Ta có: BI+IM=BM
CH+HM=CM
mà BI=CH và BM=CM
nên IM=HM
=>M là trung điểm của IH
Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên AM\(\perp\)BC
=>AM//KI//FH
Xét hình thang FHIK có
M là trung điểm của HI
MA//KI//FH
Do đó: A là trung điểm của KF

a,xét tgiac abk vuông tại k và tgiac ach vuông tại h có : góc bac chung,ab=ac(do tgiac abc cân tại a) =>tgiac abk=tgiac ach ( ch-gn) =>ak=ah( cặp cạnh tương ứng) xét tgiac ahk có ak=ah(cmt)=>tgiac ahk cân tại a b,ta có ah và bk là đường cao , cắt nhau tại i => i là trực tâm => AI cũng là đường cao mà trong tgiac cân, đường cao đồng thời là đường phân giác=> AI cũng là phân giác góc bac(đpcm) c,AI là đường cao tgiac abc => cũng là đường cao tgiac ahk => AI vuông góc hk,bc => hk song song bc ( từ vuông góc->song song)
vài chỗ tui trình bày k ok lắm nên bạn nên trình bày lại theo cách của bạn nhé .-.
a, xét tam giác AKB và tam giác AHC có : góc A chung
AB = AC do tam giác ABC cân tại A (gt)
góc AKB = góc AHC = 90
=> tam giác AKB = tam giác AHC (ch-gn)
=> AH = AK (Đn)
=> tam giác AHK cân tại A (Đn)
b, xét tam giác AHI và tam giác AKI có : AI chung
AH = AK (câu a)
góc AHI = góc AKI = 90
=> tam giác AHI = tam giác AKI (ch-cgv)
=> góc HAI = góc KAI (đn) mà AI nằm giữa AH và AK
=> AI là pg của góc HAK (đn)
c, tam giác AHK cân tại A (câu a) => góc AHK = (180 - góc A) : 2
tam giác ABC cân tại A (gt) => góc ABC = (180 - góc A) : 2
=> góc AHK = góc ABC mà 2 góc này đồng vị
=> HK // BC (đl)

AB = AC => Tam giác ABC cân tại A
a. Xét tam giác AMB và tam giác AMC
AB = AC ( gt )
Góc B = góc C ( ABC cân )
BM = CM ( gt )
Vậy...... ( c.g.c)
=> góc BAM = góc CAM ( 2 góc tương ứng )
=> AM là phân giác góc A
b. trong tam giác cân ABC đường phân giác cũng là đường cao
=> AM vuông BC
c.tam giác MEF là tam giác cân vì:
xét tam giác vuông BME và tam giác vuông CMF
Góc B = góc C
MB = MC ( gt )
Vậy....( cạnh huyền. góc nhọn )
=> ME = MF ( 2 cạnh tương ứng )
Chúc bạn học tốt !!!
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M

a) M là trung điểm của BC
=> BM=CM
tam giác ABC cân tại A
=> AB=AC
xét tam giác ABM và tam giác ACM có
AB=AC
BM=CM
cạnh AM chung
do đó : tam giác ABM= tam giác ACM ( c.c.c)
b) do tam giác ABM = tam giác ACM
=> góc A1 = góc A2
xét tam giác AEM và tam giác AFM có
cạnh AM chung
góc A1= góc A2
góc AEM=góc AFM =90 độ
do đó tam giác AEM = tam giác AFM ( cạnh huyền - góc nhọn)
c) gọi N là giao của AM va EF
do tam giác AEM= tam giác AFM
=> AE=AF
xét tam giác AEN và tam giác AFN có
cạnh AN chung
góc A1 = góc A2
AE=AF
do đó tam giác AEN=tam giác AFN ( c.g.c)
=> góc N1=góc N2
mà góc N1 + góc N2 = 180 độ ( kề bù)
=> góc N1= góc N2=90 độ
=> AN vuông góc EF
hay AM vuông góc EF
a) Xét tam giác AME vuông tại E và tam giác AMF vuông tại F có:
\(\widehat{BAM}=\widehat{CAM}\)(AM là phân giác của \(\widehat{BAC}\))
AM:chung
Suy ra \(\Delta AME=\Delta AMF\)(cạnh huyền- góc nhọn)(1)
=> ME=MF(2 cạnh tương ứng)
Suy ra MEF cân.
b)Theo đề bài: tam giác ABC có M là trung điểm BC và AM là phân giác góc BAC. Suy ra AM vừa là đường trung tuyến vừa là đường phân giác của tam giác ABC và tam giác ABC là tam giác cân.(2)
c)Từ (2)suy ra AM là đường cao của tam giác cân ABC và \(AM\perp BC\)(3)
Từ (1) ta cũng suy ra AE=AF (2 cạnh tương ứng) và AEF là tam giác cân. Xét:
\(\widehat{AEF}=\widehat{AFE=}\frac{180^o-\widehat{A}}{2}\left(4\right)\)
\(\widehat{B}=\widehat{C}=\frac{180^o-\widehat{A}}{2}\left(5\right)\)(ABC là tam giác cân(cmt))
Từ (4) và (5), suy ra các cạnh trên bằng nhau. Mà chúng lại ở vị trí so le trong nên EF//BC(6)
Từ (3) và (6), suy ra \(AM\perp EF\)(đpcm)