Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

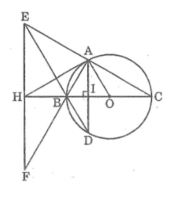
Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên: HA = HE = HF = (1/2).EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.

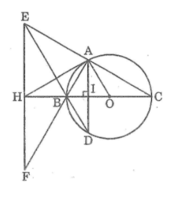
Gọi I là giao điểm của AD và BC
Vì BC là đường trung trực của AD nên theo tính chất đường trung trực ta có:
BA = BD
Tam giác BAD cân tại B có BI ⊥ AD nên BI là tia phân giác của góc ABD
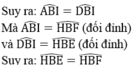
Tam giác EBF có BH là tia phân giác của góc EBF và BH ⊥ EF nên tam giác EBF cân tại B.

Gọi BF,CE cắt nhau tại K và cắt AC,AB lần lượt tại S,T. Đường thẳng AH cắt MF,ME lần lượt tại P,Q.
Ta dễ thấy P là trực tâm của \(\Delta\)MAC, suy ra CP // EA (Cùng vuông góc AM). Tương tự BQ // FA
Áp dụng ĐL Melelaus và ĐL Thales ta có:
\(\frac{\overline{KB}}{\overline{KF}}.\frac{\overline{TA}}{\overline{TB}}.\frac{\overline{EF}}{\overline{EA}}=1\Rightarrow\frac{\overline{TA}}{\overline{TB}}=\frac{\overline{KF}}{\overline{KB}}.\frac{\overline{EA}}{\overline{EF}}=\frac{\overline{AF}}{\overline{QB}}.\frac{\overline{EA}}{\overline{EF}}\)
\(\frac{\overline{KC}}{\overline{KE}}.\frac{\overline{SA}}{\overline{SC}}.\frac{\overline{FE}}{\overline{FA}}=1\Rightarrow\frac{\overline{SC}}{\overline{SA}}=\frac{\overline{KC}}{\overline{KE}}.\frac{\overline{FE}}{\overline{FA}}=\frac{\overline{CP}}{\overline{EA}}.\frac{\overline{FE}}{\overline{FA}}\)
Suy ra \(\frac{\overline{TA}}{\overline{TB}}.\frac{\overline{HB}}{\overline{HC}}.\frac{\overline{SC}}{\overline{SA}}=\frac{\overline{CP}}{\overline{QB}}.\frac{\overline{HB}}{\overline{HC}}=-\frac{\overline{HC}}{\overline{HB}}.\frac{\overline{HB}}{\overline{HC}}=-1\)
Áp dụng điều kiện đủ của ĐL Ceva ta thu được AH,BS,CT đồng quy hay AH,BF,CE đồng quy (đpcm).

Áp dụng đlí Py - ta - go cho tam giác BAO vuông tại B , ta có :
\(OA^2=OB^2+AB^2\)
\(AB^2=OA^2-OB^2=5^2-3^2=16\)
\(AB^2=16\Rightarrow AB=4cm\)
=> AC = 4cm
Theo tính chất 2tt cắt nhau , ta có :
DB = DM ; EC = EM
=> AD + DE + AE = AB + AC = 4 + 4 = 8
Vậy : chu vi tam giác ADE là : 8cm