Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Bước sóng ![]() .
.
Khoảng cách lớn nhất từ CD đến AB mà trên CD chỉ có 3 điểm dao động với biên độ cực đại khi tại C và D thuộc các vân cực đại bậc 1.
Tại C: ![]()

![]()
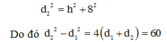
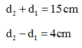
Suy ra ![]()


Bước sóng: \(\lambda=\dfrac{v}{f}=\dfrac{30}{20}=1,5cm\)
Trên CD có 5 cực đại và khoảng cách từ CD đến AB là lớn nhất, suy ra mép C, D thuộc cực đại thứ 2.
\(\Rightarrow CB-CA =2\lambda=3cm\)
\(HO=CI=6/2=3cm\)
\(AH=7-3=4(cm)\)
\(BH=7+3=10(cm)\)
Ta có: \(CB^2=HB^2+CH^2=10^2+CH^2\) (1)
\(CA^2=AH^2+CH^2=4^2+CH^2\) (2)
Lấy (2) - (1) vế với vế \(\Rightarrow CB^2-CA^2=10^2-4^2=84\)
\(\Rightarrow (CB-CA)(CB+CA)=84\)
\(\Rightarrow CB+CA = 84:3 = 28\)
Có: \(CB-CA=3\)
\(\Rightarrow CB = 15,5(cm)\)
\(\Rightarrow CH=\sqrt{CB^2-HB^2}=\sqrt{15,5^2-10^2}=11,84cm\)
Chọn A.

Đáp án C
+ Điều kiện để có cực đại giao thoa với hai nguồn ngược pha
∆ d = d 2 - d 1 = ( k + 0 , 5 ) λ .
Với khoảng giá trị của ∆ d :
0 - 14 , 5 cm < ∆ d < 10 , 875 - 3 , 625 cm → - 7 , 75 ≤ k ≤ 3 , 125 .
→ Có 11 điểm dao động với biên độ cực đại.

Đáp án C
+ Hai nguồn ngược pha, có bước sóng: λ = v f = 40 20 = 2
+ A P = 3 4 A B = 10 , 875 ; B P = 1 4 A B = 3 , 625 c m
+ Số điểm dao động với biên độ cực đại trên đoạn AP thỏa mãn biểu thức sau:
− A B < k + 1 2 λ ≤ A P − B P ⇔ − 14 , 5 < k + 1 2 2 ≤ 7 , 25
→ 7 , 75 < k < 3 , 125 → k = − 7 ; − 6 ; − 8 ; − 4 ; ± 3 ; ± 2 ; ± 1 ; 0
→ Vậy có 11 điểm dao động với biên độ cực đại trên AP

Bài này nhé: Câu hỏi của xàm xàm - Vật lý lớp 12 | Học trực tuyến





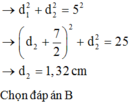
chọn đáp án D
Theo đề bài thì ta thấy ABCD sẽ được lập thành 1 hình thang cân, Đáy lớn là AB, đáy nhỏ CD. Chiều cao H là đáp án cần tìm.Để cho trên đoạn CD chỉ có 3 điểm dao động cực đại thì đồng nghĩa chỉ có 2 hypebol giao CD (1 còn lại là vân trung tâm) vậy thì CD giao các hepybol K=1
Lúc này , để các điểm đó là cực đại thì D 2 - D 1 = K λ , ta sẽ xác định tọa độ C và D rồi lồng vào bất đẳng thức sau
B D - A D ≤ k λ ≤ B C - A C các độ dài của đoạn BC, AC hay các đoạn thành phần của AB các bạn vẽ hình ra để thấy cho rõ nhé !
Ta thấy H chỉ nhỏ nhất khi CB-AC nhỏ nhất
⇔ B C - A C = 1 . 5 ( 1 )
ta lại có :
B C 2 = H 2 + 6 2 ( 2 )
và A C 2 = H 2 + 2 2 ( 3 )
Áp dụng hằng đẳng thức : A 2 - B 2 để lấy (2) - (3) ,tiếp đến lấy phương trình (1) thế vào phương trình vừa tính ta được
( A C + B C ) = 32 1 . 5
Giải hệ (1) và (4) ta tìm được BC và AC , từ đó tìm được H = 9.7